Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 37
37. Determine a força nos membros , e da treliça Warren Indique se os membros estão sob tração ou compressão.
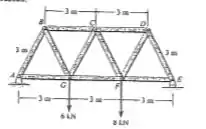
Passo 1
Para começar a resolver o problema, primeiro vamos analisar o digrama de corpo livre a seguir:
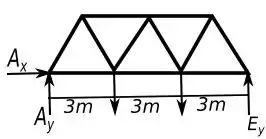
Observando o digrama, vemos que será necessário determinar , já que ele influencia os membros que queremos determinar e vamos fazer isso através da equação de equilíbrio do momento no ponto , pois assim e não contribuem para essa conta.
Após isso a gente vai analisar o equilíbrio em alguns nós pra gente encontrar os esforços. A nossa meta é chegar nos nós D para achar a força em DC, e no nó F para achar as forças em CF e FG então vamos começar pelo nó E.
Passo 2
Vamos determinar :
E com isso a gente pode olhar pro nó E:
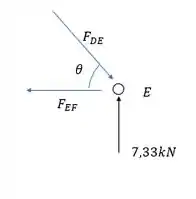
Detalhe que aqui os esforços que estão no sentido de comprimir o nó são de compressão(C) e os esforços que saem do nó são de tração(T). Aqui a gente arbitrou no desenho e se o sinal trocar nas contas a gente troca o sentido, ok?
Como todos os triângulos são equiláteros então o ângulo vale:
E com o equilíbrio do nó a gente tem:
E aí, substituindo:
E pelo equilíbrio das forças horizontal:
E substituindo de novo:
Passo 3
Chegando no nó D, a gente vai ter:
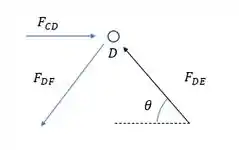
Se liga aqui, nós precisamos sempre buscar eliminar uma incógnita e nesse nó o jeito é começar pelo equilíbrio das forças em y.
Pela simetria da treliça, a gente tem o mesmo ângulo para FDF
E com isso:
Encontramos FCD.
Passo 4
Por fim a gente vai partir pro nó F, para achar os esforços em CF e FG:
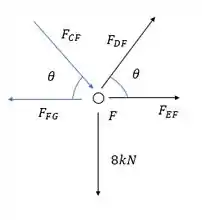
Galerinha, a nossa única saída é começar pelo somatório das forças em y, pois em x teremos duas incógnitas.
Nós representamos como compressão mas o sinal deu negativo o que significa que é tração e é representado melhor assim:
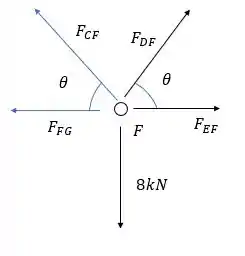
E por fim, no mesmo nó
E substituindo geral: