Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 30
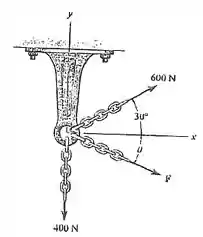
2.30. Três correntes atuam sobre o suporte, de modo a criarem uma força resultante com intensidade de Se duas das correntes estão submetidas a forças conhecidas como mostra a figura, determine o ângulo θ da terceira corrente, medida no sentido horário a partir do eixo x positivo, de modo que a intensidade da força F nessa corrente seja mínima. Todas as forças estão localizadas no plano x-y. Qual é a intensidade de F? Dica : Determine primeiro a resultante das duas forças conhecidas. A força F atua nessa direção.
Passo 1
Fala, querido. Aqui ele quer duas coisas. Ele quer a orientação de e quer também o valor dela.
Mas o fofo já dá um bizu: atua na resultante das forças conhecidas.
Agora pensa comigo. Se está na resultante das forças conhecidas, a resultante das três forças juntas vai estar em que direção?
Só pensar, a resultante das 3 forças é a resultante das duas forças conhecidas (que atua na direção de ) mais a força . Temos então duas forças somadas na mesma direção. A resultante delas vai ficar nessa mesma direção! O que nos diz que está na direção de .
Então, vamos seguir o bizu do enunciado e achar a orientação de , e depois o que ele pede.
Passo 2
Vamos começar calculando que é a resultante de , como a dica do exercício diz.
Vamos fazer um esqueminha dessa soma vetorial:
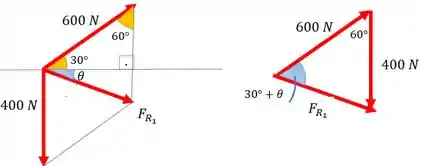
Pela lei dos cossenos, tiramos que:
Passo 3
Agora podemos usar a lei dos senos para calcular o ângulo θ
Passo 4
Agora podemos calcular a intensidade mínima para F. Lembra que F e tinham a mesma direção? Então podemos escrever: