Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 19

Expresse o vetor posição r A B na forma de um vetor cartesiano; depois determine sua intensidade e seus ângulos de direção coordenados.

Passo 1

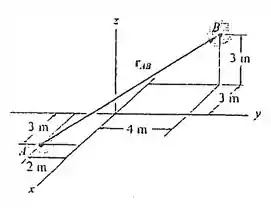
Vamos começar encontrando as coordenadas dos pontos de início e fim do nosso vetor:

A 3 ,   - 2 ,   0   m

B - 3 ,   4 ,   3   m

E definimos nosso vetor pela subtração entre os pontos final e inicial com seus devidos vetores unitários:

r A B = { - 3 - 3 i + 4 - ( - 2 ) j + 3 - 0 k }

r A B = - 6 i + 6 j + 3 k   m

Passo 2

E podemos encontrar a intensidade do nosso vetor:

r A B = - 6 2 + 6 2 + 3 2

r A B = 9   m

Passo 3

Por último, determinamos os ângulos de direção coordenados pela relação:

α = cos - 1 ⁡ r x r

β = cos - 1 ⁡ r y r

γ = cos - 1 ⁡ r z r

Então:

α = cos - 1 ⁡ - 6 9 ∴ α = 132 °

β = cos - 1 ⁡ 6 9 ∴ β = 48,2 °

γ = cos - 1 ⁡ 3 9 ∴ γ = 70,5 °

Resposta

r A B = - 6 i + 6 j + 3 k   m

r A B = 9   m

α = 132 °

β = 48,2 °

γ = 70,5 °

Ver Outros Exercícios desse livro