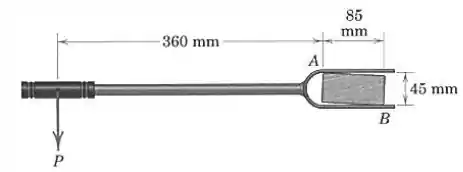
A ferramente mostrada é usada para endireitar peças torcidas ao final de uma montagem com madeira. Se a força P = 150N é aplicada ao cabo como mostrado, determine as forças normais aplicadas à garra nos pontos A e B . Despreze o atrito.

Os módulos das forças normais são N A = 785N e N B = 635N .

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 100

A ferramente mostrada é usada para endireitar peças torcidas ao final de uma montagem com madeira. Se a força é aplicada ao cabo como mostrado, determine as forças normais aplicadas à garra nos pontos e . Despreze o atrito.

Passo 1

Dê uma olhada na imagem: a ferramenta só está em contato com a peça por dois pontos e , e em cada um desses pontos teremos uma força de contato, que vamos chamar de e . Essas são as forças que atuam sobre a ferramenta, não sobre a peça.

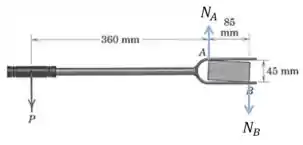
Beleza, são apenas duas variáveis desconhecidas, então precisamos de duas equações de equilíbrio.

Começamos com o momento em relação ao ponto (poderia ser o também, o importante é que uma das normais tenha momento nulo nessa equação):

Passo 2

Agora que só ficamos com uma única força desconhecida, vamos aplicar a condição de equilíbrio das forças na direção vertical:

E então essas são as forças aplicadas à garra nos pontos e , e elas têm os mesmos sentidos que nós representamos no desenho.

Resposta

Os módulos das forças normais são e .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe o diagrama de corpo livre para os problemas a seguir.A treliça no Problema 5.10 .A viga no Problema 5.11 .A viga no Problema 5.12 .A viga no Problema 5.14 .

Desenhe o diagrama de corpo livre para os problemas a seguir.A viga no Problema 5.1 5 .A tábua no Problema 5.1 6 .A haste no Problema 5.1 7 .O bastão de vidro no Problema 5 . 18 .

Desenhe o diagrama de corpo livre para os problemas a seguir.O elemento no Problema 5.1 9 .A porteira no Problema 5 . 20 .A alavanca A B C no Problema 5 . 21 .A viga no Problema 5 . 22 .

Desenhe o diagrama de corpo livre para os problemas a seguir.O elemento em " L " no Problema 5 . 25 .O guindaste e a lança no Problema 5 . 26 .O elemento no Problema 5 . 27 .A haste no Problema 5 . 28

Desenhe o diagrama de corpo livre para os problemas a seguir.A viga no Problema 5 . 52 .O menino e o trampolim no Problema 5 . 53 .O conjunto da plataforma no Problema 5 . 54 .A haste no Problema 5 .