Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 102
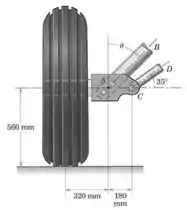
Os projetistas do trem de pouso de um avião desejam fazer com que as forças em ambos os eixos e atuem ao longo de seus respectivos comprimentos. Que ângulo eles devem especificar para o eixo ? Os pesos e todos os elementos são pequenos comparados às forças que atuam no sistema mostrado. Trate como um problema bidimensional.
Passo 1
O que significa fizer que as forças têm que atuar ao longo dos comprimentos dos eixos? A ideia é a seguinte: se uma força não estiver alinhada com o comprimento do eixo, a tendência será que o eixo “gire” em torno do seu ponto fixo até que esteja alinhado à força. É isso que queremos evitar.
Podemos resumir isso em uma afirmação só: queremos que o momento total sobre o sistema seja nulo.
Uma forma de garantir isso é, além de todas as forças estarem em equilíbrio em cada direção, que todas as linhas e ação das forças se cruzem em algum ponto.
Passo 2
Como estamos preocupados com o ângulo , e não sabemos os módulos das forças, precisamos apenas garantir a segunda condição.
Além das duas forças e nos eixos, temos uma força normal agindo sobre a roda, vamos desenhar um caso em que as linhas dessas três forças se cruzam, e então procurar o valor de que satisfaz isso:
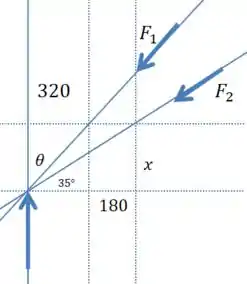
Podemos encontrar o valor de usando o ângulo de que foi dado pelo enunciado:
E a partir daí fica fácil calcular o ângulo :
Resposta
O ângulo deve ser .