Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 8
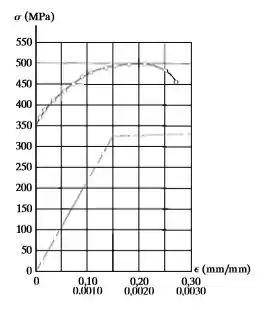
A figura apresenta o diagrama tensão-deformação de uma barra de aço. Determine os valores aproximados do módulo de elasticidade, limite de proporcionalidade, limite de resistência e módulo de resiliência. Se a barra for submetida a uma carga de tração de , determine o valor da recuperação da deformação elástica e da deformação permanente na barra quando descarregada.
Passo 1
Falaaaa! Vamos entender esse gráfico aí. O de baixo é o começo do diagrama. E o de cima é a continuação, para tensões maiores. Os dois representam o mesma material, beleza?
O limite de proporcionalidade do material é o ponto do diagrama imediatamente antes da mudança do coeficiente linear da reta, pois temos que a curva é linear entre a origem e o ponto. Portanto:
Para calcularmos o módulo de elasticidade, podemos usar os valores de e de qualquer ponto do diagrama que siga a Lei de Hooke, ou seja, que estejam dentro da reta. Aí a gente tem:
Substituindo na Lei de Hooke
Passo 2
Agora vamos calcular o módulo de resiliência do nosso material. Para isso, vamos lembrar que ele é igual à área da região linear do diagrama Tensão-Deformação. Ou seja:
Passo 3
O limite de elasticidade é dado pela curva no gráfico. Até o limite de proporcionalidade nossa curva é reta, e depois ela começa a variar pouco.
Nesse intervalo a gente ainda pode ter um comportamento elástico, mesmo fora do regime linear elástico.
Mas repara, que na parte seguinte a curva começa a crescer muito rápido de uma forma mais parecida com uma parábola. O começo desse último intervalo vai ser nosso limite de elasticidade:
Passo 4
Aqui a gente olha para o gráfico de cima. Ele representa a aplicação de uma carga adicional depois que o escoamento tiver terminado. Ele mostra o comportamento do endurecimento por deformação.
Aí o limite de resistência é dado pelo pico desse gráfico
Passo 5
O valor aproximado de recuperação elástica é dado pela deformação atingida durante o intervalo onde nosso material se comporta de forma elástica, ou seja, até o limite de elasticidade. A gente acha ele pela fórmulinha:
E a deformação permanente é a deformação que fica depois que ele se recupera, em relação a deformação que ele atingiu.