Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 20
A figura mostra o diagrama tensão-deformação de duas barras de poliestireno. Determine a área da seção transversal de cada barra de modo que elas sofram ruptura simultânea quando a carga é aplicada. Considere que não ocorra nenhuma flambagem.
Passo 1
Oláaa, querido! Tá bem?
Então, ele deu esse gráfico que mostra o comportamento do material que forma a estrutura. O gráfico mostra que a tensão de ruptura quando o material está sob compressão é e a tensão de ruptura para a tensão de tração é .
Aí ele quer saber as seções transversais de cada barra para que ambas estejam na eminência de ruptura quando .
Como a gente faz isso? Bem, a gente vai descobrir a força normal interna em cada uma das barras, vê qual está em tração e qual está em compressão. E usar essas tensões limites para saber o valor da área transversal de cada uma.
Bora lá!
Passo 2
Primeira coisa é achar as forças nas barras. Olha nosso diagrama de corpo livre:
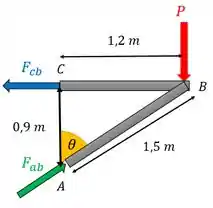
Percebe que a gente colocou as forças que queremos achar logo na direção das forças normais a cada barra, e na seção cortada de cada barra. Aí fica mais tranquilo ver quem é força de compressão e quem é de tração.
E que a gente viu que o comprimento de é , porque é um triângulo do tipo 3/4/5.
Passo 3
Vamos aplicar a equação de momento para considerando o anti-horário positivo:
O seno a gente acha pelo triângulo . Dele temos que
Substituindo:
Percebe que como deu positivo, a orientação que a gente escolheu é a real. E como o nosso vetor entra na seção da barra, ela é uma força de compressão.
Passo 4
Agora o equilíbrio na direção horizontal:
Substitiundo a expressão de que temos:
Como deu positivo, nosso vetor está na direção certa. E já que ele sai da seção, temos tração em .
Passo 5
Belezinha, agora que a gente tem a expressão das forças em cada barra, vamos achar as áreas tranversai de cada uma.
A barra está sofrendo compressão, então a tensão de ruptura dela é
A ideia é que ela esteja na eminência de romper, então a tensão média nela é essa tensão de compressão limite:
Substituindo as expressões que a gente tem e isolando :
Repara que usando e o resultado sai em 😉
Passo 6
Fazendo o mesmo para sabendo que ela está em tração, então:
Substituindo as expressões que a gente tem e isolando :