Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 17
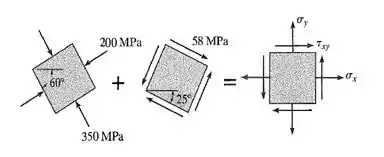
17. Um ponto sobre uma chapa fina está sujeito aos dois estados de tensão sucessivos mostrados na figura. Determine o estado de tensão resultante representado no elemento orientado como mostrado à direita.
Passo 1
Fala aí galerinha do RespondeAí! Tudo certinho?
Bom! A questão dá dois elementos orientados de diferentes ângulos, e pede o estado de tensão resultante dos dois.
Como mostrado na própria figura, com aquele símbolo de o que temos que fazer é girar os dois elementos para caírem na orientação do terceiro e depois somar as tensões que aparecerem em cada componente.
Bora!
Passo 2
Vamos lá calcular as tensões para o primeio elemento! Da figura do enunciado, obtemos que o estado plano nos fornece os seguintes dados:
, com valor negativo, uma vez que é uma tensão normal de compressão.
, com valor negativo, uma vez que é uma tensão normal de compressão.
, uma vez que não aparecem as famosas setas de tensão cisalhantes na nossa figura.
Ao olhar nossa figura do enunciado vemos que ela faz um ângulo de com a horizontal.
Temos então, que para deixar esse elemento na orientação do terceiro, vamos rotacioná-lo de um ângulo , no sentido anti-horário, portanto, positivo.
Para ver isso, você pode imaginar que pegou o quadradinho na mão. E vai girar ele para ficar com a orientação do teceiro quadradinho. Aí você olha em que sentido ele girou. Cê pode tanto girar ele no sentido horário de ou no anti-horário de como fizemos. Beleza? Bora!
Passo 3
Ora bolas! Vamos, então, aplicar as fórmulas de transformação de tensão que já conhecemos, para encontrar nossos valores no primeiro elemento:
E sabemos também o valor das seguintes variáveis:
Por fim, só nos resta substituir esses valores nas três expressões das tensões acima, para encontrar quanta vale cada uma.
E encontramos que:
Passo 4
Em seguida, vamos determinar as tensões para o outro elemento. Analisando a figura do enunciado, tiramos os seguintes dados no estado plano desse elemento:
, uma vez que não há nenhuma tensão normal na horizontal
, uma vez que não há nenhuma tensão normal na vertical.
, com valor positivo, uma vez que as setas de tensão cisalhante estão apontando para o primeiro e terceiro quadrantes.
Ao olhar nossa figura do enunciado vemos que ela faz um ângulo de com a horizontal.
Temos então, que para deixar esse elemento na orientação do terceiro, vamos rotacioná-lo de um ângulo , no sentido anti-horário, portanto, positivo.
Passo 5
Basta, então, que apliquemos novamente as fórmulas de transformação de tensão que já conhecemos, para encontrar nossos valores pro segundo elemento:
E sabemos também o valor das seguintes variáveis:
Por fim, só nos resta substituir esses valores nas três expressões das tensões acima, para encontrar quanta vale cada uma:
E encontramos que:
Passo 6
Para encontrar as tensões resultantes, basta agora somar os resultados obtidos nos e. Bora lá, que tá quase acabando!
Substuindo os valores obtidos, temos que:
E chegamos até:
Resposta
Tensões resultantes: