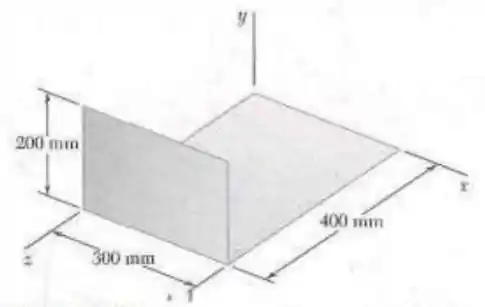
Uma seção de chapa de aço de de espessura é cortada e dobrada para formar o componente de máquina mostrado na figura. Sabendo que a massa específica do aço é , determine os produtos de inércia do componente.

Primeiramente vamos dividir a nossa peça em duas partes onde a placa na vertical chamaremos de e a placa na horizontal chamaremos de . Então, calculemos suas respectivas massas

Para cada painel, temos que o produto de inércia para o centroide é zero em relação ao par de eixos coordenados. Podemos criar a seguinte tabela com os dados que temos e os dados que podemos inferir da imagem

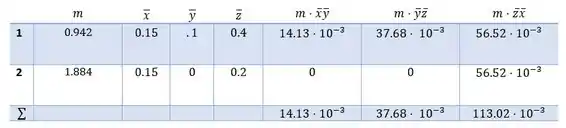
Assim, nossos produtos de inércia serão dados por