Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 167

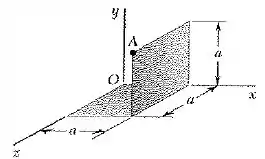
Na figura é mostrada uma placa delgada dobrada de massa específica uniforme e peso W. Determine seu momento de inércia de massa em relação à linha que liga a origem O e o ponto A.

Passo 1

Antes vamos separar cada componente, de tal modo que:

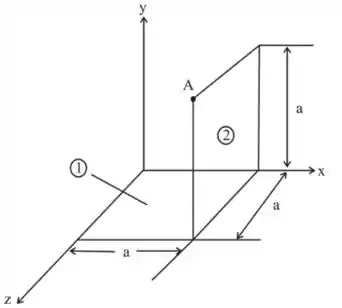
Passo 2

Agora, que separamos cada parte, vamos computar a massa de cada componente. Note que os componentes têm a mesma medida, portando a mesma massa, assim

m 1 = m 2 = 1 2 W g  

Precisamos também do vetor dos cossenos diretores, λ O A . Note que se traçarmos linha no eixo OA vamos obter 3 ângulos entre os eixos coordenados, cujo cossenos deles são 3 3 . Portanto,

λ O A = 3 3 ( i + j + k )

Passo 3

Certo! Agora vamos utilizar o teorema dos eixos paralelos e como o formato da figura é retangular, podemos utilizar os momentos de inércia conhecidos. Em relação ao eixo x, temos que

I x = I x 1 + I x 2

I x = 1 12 1 2 W g   a 2 + 1 2 W g a 2 2 + 1 12 1 2 W g a 2 + a 2 + 1 2 W g a 2 2 + a 2 2

I x = 1 2 W g 1 12 + 1 4 a 2 + 1 6 + 1 2 a 2

I x = 1 2 W g a 2

Para o eixo y, temos

I y = I y 1 + I y 2

I y =   1 12 1 2 W g a 2 + a 2 + 1 2 W g a 2 2 + a 2 2 + 1 12 1 2 W g a 2 + 1 2 W g a 2 + a 2 2  

I y =   1 2 W g 1 6 + 1 2 a 2 + 1 12 + 5 4 a 2

I y = W g a 2

No eixo z

I z = I z 1 + I z 2

I z = 1 12 1 2 W g   a 2 + 1 2 W g a 2 2 + 1 12 1 2 W g a 2 + 1 2 W g a 2 + a 2 2

I z = 1 2 W g 1 12 + 1 4 a 2 + 1 12 + 5 4 a 2

I z = 5 6 W g a 2

Passo 4

Certo, agora que já sabemos o momento de inércia com relação a cada eixo, vamos calcular o produto de inércia. Observe que os produtos de inércia I x ' y ' , I y ' z ' e I z ' x ' são zero, por causa da simetria. Então,

I x y = ∑ I x ' y ' + m x - y -

I x y = m 2 x - 2 y - 2

I x y = 1 2 W g a a 2 = 1 4 W g a 2

Do mesmo modo,

I y z =   ∑ I y ' z ' + m y - z -

I y z =   m 2 y - 2 z - 2

I y z = 1 2 W g a 2 a 2 = 1 8 W g a 2

Por último

I z x =   ∑ I z ' x ' + m z - x -

I z x =   m 1 z - 1 x - 1 + m 2 z - 2 x - 2

I z x = 1 2 W g a 2 a 2 + 1 2 W g a a 2   = 3 8 W g a 2

Passo 5

Agora com os momentos de inércia dos eixos e os produtos de inércia calculados, só basta substituir na equação abaixo que teremos nossa resposta

Note que,

Substituindo, teremos

I O A = 1 3 1 2 W g a 2 + W g a 2 + 5 6   W g a 2 - 2 1 4 W g a 2 + 1 8 W g a 2 + 3 8   W g a 2

I O A = 1 3 14 6 - 2 3 4 W g a 2

I O A = 5 18 W g a 2

Resposta

I O A = 5 18 W g a 2

Ver Outros Exercícios desse livro