Um fluido com densidade escoa por uma tubulaçăo de aço em balanço de comprimento e área de seção transversal (Figura 3.60). Determine a velocidade ( ) do fluido à qual ocorre instabilidade. Admita que a massa total e a resistência à curvatura da tubulação são e , respectivamente.
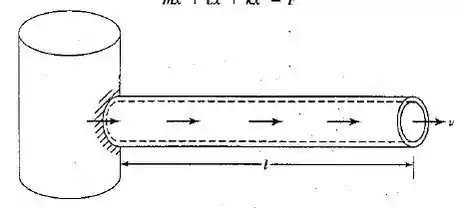
Passo 1
Modele o tubo como um sistema de único grau de liberdade com massa equivalente no final massa do tubo ; veja o problema e .
Inclinação do tubo no fim:
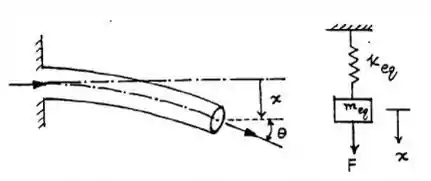
onde x = deflexão final do tubo cantilever sob uma carga transversal F. Força induzida devido à velocidade do fluido v é . Força atuando no sistema de grau único de liberdade (na direção vertical):
Equação do movimento: ou
Instabilidade ocorre em