Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.3 - Ex. 9
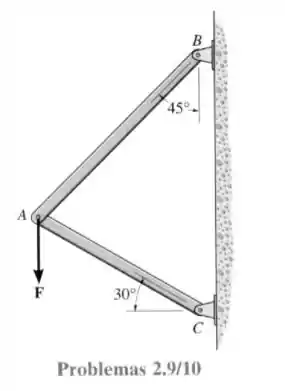
9- A força vertical atua para baixo em nos dois elementos da estrutura. Determine as intensidades dos dois componentes de orientados ao longo dos eixos de e . Considere que .
Passo 1
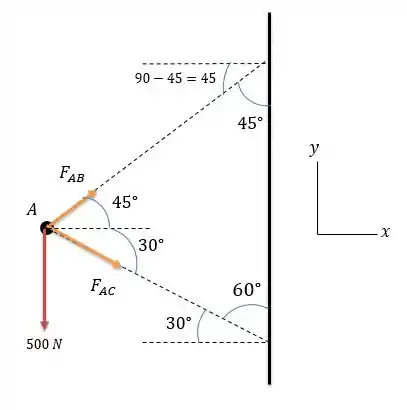
Quando se tem uma força que se encontra no ponto tal como na figura nós consideramos que existem forças paralelas as barras tal como mostrado na figura abaixo que também saem desse ponto.
Passo 2
Fazendo a somatória das forças no ponto deveremos ter para que o sistema fique estático. Logo em temos:
Agora para a somatória das forças em .
Passo 3
Isolando na segunda equação temos:
Agora aplicando essa força na primeira equação temos:
Dessa forma:
Isso nos diz que a força está no sentido contrário ao que foi desenhado.
Agora podemos calcular ao se usar o valor de na primeira equação desse passo:
Mesma coisa, o sentido está ao contrário ao que foi desenhado. Como a questão quer só o valor isso não importa muito.