Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 52

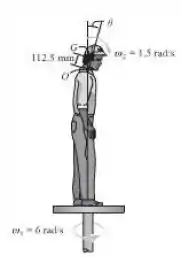
O homem está parado sobre a mesa giratória que gira em torno de um eixo vertical com uma velocidade angular constante ω 1 = 6   r a d / s . Se ele inclina sua cabeça para frente a uma velocidade angular constante ω 2 = 1,5   r a d / s em torno do ponto O , determine a intensidade do momento que deve ser resistido por seu pescoço em O no instante θ = 30 ° . Suponha que sua cabeça pode ser considerada como uma esfera uniforme de 5   k g tendo um raio de 112,5   m m e centro de gravidade localizado em G , e o ponto O na superfície da esfera.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Ao rotacionar a cabeça, a angulação irá gerar componentes da velocidade angular ω 1 = 6   r a d / s .

São elas:

ω 1 = 6 cos ⁡ 30 ° j + 6 sin ⁡ 30 ° k

ω 1 = 5,196 j + 3 k

Do enunciado, temos que ω 2 = 1,5   r a d / s , portanto, o vtetor velocidade resultante do sistema neste momento é:

ω = ω 1 + ω 2

ω = - 1 , 5 i + 5 , 196 j + 3 k

A aceleração angular da cabeça ω ˙ com relação ao eixo x y z pode ser obtida considerando um novo eixo x ' y ' z ' que tem uma velocidade angular de Ω ' = ω 1 = 5,196 j + 3 k . Portanto:

ω ˙ = ω ˙ x ' y ' z ' + Ω ' × ω

Podemos dividir da seguinte forma:

ω ˙ = ω ˙ 1 x ' y ' z ' + ω ˙ 2 x ' y ' z ' + Ω ' × ω 1 + Ω ' × ω 2

ω ˙ = 0 + 0 + 0 + 5,196 j + 3 k × - 1,5 i

ω ˙ = - 4,5 j + 7,794 k   r a d / s 2

As componentes são dadas por:

ω ˙ x = 0

ω ˙ y = - 4,5   r a d / s 2

ω ˙ z = 7,794   r a d / s 2

Os momentos de inércia são dados por:

I x = I z = 2 5 5 0,1125 2 + 5 0,1125 2

I x = I z = 0,0886   k g ⋅ m 2

I y = 2 5 5 0,1125 2

I y = 0,0253   k g ⋅ m 2

Agora temos todos os dados necessários para calcular o momento gerado na cabeça. Ele é dado por:

∑ M x = I x ω ˙ x - I y - I z ω y ω z

M x - 5 sin ⁡ 30 ° ( 0,1125 ) = 0 - 0,0253 - 0,0886 ( 5,196 ) ( 3 )

M x = 1,268   N ⋅ m

∑ M y = I y ω ˙ y - I z - I x ω x ω z

M y = 0,0253 ( - 4,5 ) - 0

M y = - 0,11385   N ⋅ m

∑ M z = I z ω ˙ z - I x - I y ω x ω y

M z = 0,0886 ( 7,794 ) - 0,0886 - 0,0253 ( - 1,5 ) ( 5,196 )

M z = 1,184   N ⋅ m

A resultante será:

M A = M x 2 + M y 2 + M z 2

M A = 1,268 2 + - 0,11385 2 + 1,184 2

M A = 1,74   N ⋅ m

Resposta

M A = 1,74   N ⋅ m

Ver Outros Exercícios desse livro