Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 51
O reboque com sua carga tem uma massa de 150 kg e um centro de massa em G. Se ele é submetido a uma força horizontal P = 600 N, determine a aceleração do reboque e a força normal sobre o par de rodas em A e em B. As rodas estão livres para rodar e têm massa desprezível.
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Vamos começar o exercício aplicando o somatório de forças na direção x com base na ilustração a seguir:
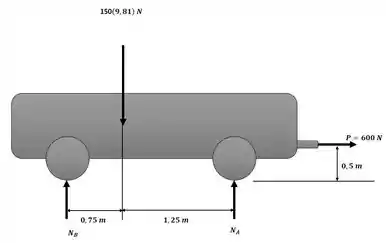
Passo 2
Agora usaremos o resultado do passo 1 para aplicar a equação de momento ao redor do ponto A para descobrir a reação em B:
Passo 3
Agora, iremos usar os resultados dos passos 1 e 2 para aplicar o somatório de forças na direção y e descobrir o valor da reação em A:
Resposta
Exercícios de Livros Relacionados
A nave espacial está girando em torno do seu eixo z , que possui uma orientação espacial fixa, na taxa constante p = 1 / 10r a d / s . Simultaneamente, os seus painéis solares estão se desdobrando à t
O centro O da nave espacial está se deslocando através do espaço com uma velocidade constante. Durante o período do movimento anterior à estabilização, a nave espacial possui uma taxa de rotação const
O disco circular com 100 mm de raio gira em torno de seu eixo z com a velocidade constante p = 240r p m , e o braço O C B gira em torno do eixo Y na velocidade constante N = 30r p m . Determine a velo
Para as condições descritas no Exemplo 7/2, exceto que γ está aumentando na taxa constante de 3 ⋅ πr a d / s , determine a velocidade angular ω e a aceleração angular α do rotor quando a posição γ = 3
O disco possui uma velocidade angular constante p em torno de seu eixo z , e o garfo A possui uma velocidade angular constante ω 2 em torno de seu eixo, como mostrado. Simultaneamente, o conjunto inte