Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 87
Resolva o problema 16.68 utilizando o método do centro de velocidade.
Passo 1
Vamos relembrar o Problema 16.68:
Se a barra tem uma velocidade angular rad/s, determine a velocidade do bloco deslizante no instante mostrado.
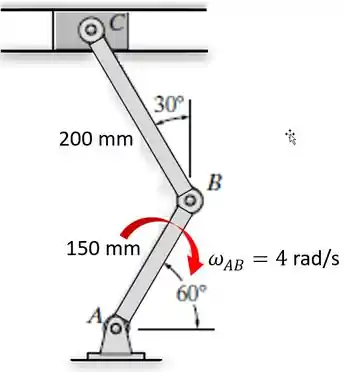
Portanto, sabemos quenos foi dado que:
Velocidade angular da barra : rad/s;
Comprimento de m;
Comprimento de : m;
Devemos determinar a velocidade do bloco no instante mostrado.
Vemos que o bloco se movimenta somente na horizontal, portanto sua velocidade terá componente somente na horizontal.
Passo 2
Vamos aplicar o método do centro de velocidade. Sabemos que, por definição, a partir do ponto de referência, a intensidade da velocidade de pontos arbitrários sobre o corpo pode ser determinada utilizando a equação
Onde é a distância radial até o ponto de centro instantâneo de velocidade nula (CI)
Vamos iniciar escolhendo o ponto como nosso CI. Logo, temos que
Onde é a velocidade do ponto e é perpendicular ao raio de ação .
Passo 3
Em seguida, vamos encontrar as distâncias do ponto e até o .
Para isso, vamos desenhar o diagrama com a localização do e as distâncias radiais dos ponto e até
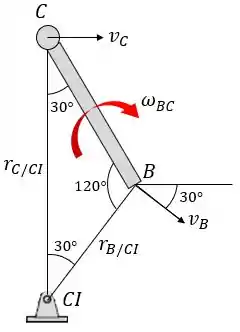
Por semelhança de triângulos, vemos que
Logo, m.
Também por semelhança de triângulos, temos que
Logo, m.
Passo 4
Agora vamos determinar a velocidade angular da barra .
Sabemos que , logo
Temos o valor de e de , portanto
Passo 5
Por fim, vamos obter o valor de .