Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 215

No instante mostrado, o carro A move-se ao longo da porção reta da estrada com uma velocidade escalar de 25 m/s. Neste mesmo instante, o carro B move-se ao longo da porção circular da estrada com uma velocidade escalar de 15 m/s. Determine a velocidade do carro B em relação ao carro A.

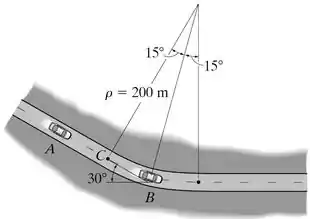
Passo 1

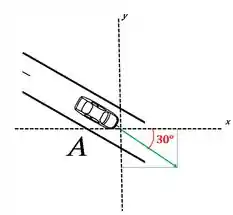
Primeiramente as velocidades dos carros A e B devem ser exepressas vetorialente de acordo com as suas coordenadas cartesianas, de forma que :

v - A = 25 cos ⁡ 30 ° i -   25 sin ⁡ 30 ° j m s =   21,65 i - 12,5 j   m / s (1)

v - B = 15 cos ⁡ 15 ° i -   15 sin ⁡ 15 ° j m s =   14,49 i - 3,88 j   m / s (2)

Passo 2

Sabendo que a equação da velocidade relativa do carro B em relação a A é dada por :

v - B = v - A + v - B / A (3)

Deve-se substituir (1) e (2) em (3), de forma que:

14,49 i - 3,88 j = 21,65 i - 12,5 j + v - B / A

v - B / A =   - 7,162 i + 8,618   j (4)

Passo 3

De acordo com os passo 2 a velocidade relativa vB/A pode ser expressa vetorialmente em (4). Ou ainda pode ser expressa de acordo com a sua magnitude e direção, de forma que :

v B / A =   ( - 7,162 ) 2 + ( 8,618 ) 2 = 11,2   m / s

θ V = tan - 1 ⁡ 8,618 7,162 = 50,3 °

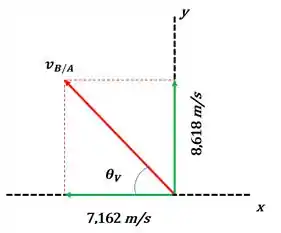
Resposta

De acordo com os passos 1, 2 e 3 a velocidade relativa do carro B em relação a A será:

v - B / A = - 7,162 i + 8,618   j   m / s

Ou ainda:

v B / A = 11,2 m s   ;   ⦩ 50,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Arbustos e galhos são colocados a uma taxa de 5k g / s no ponto A de um triturador que elimina os resíduos de madeira resultantes em C com uma velocidade de 20m / s . Determine o componente horizontal
O motor a jato mostrado na figura admite ar em A a uma taxa de 100 kg/s e o descarrega em B a uma velocidade de 600 m/s em relação ao avião. Determine a intensidade e a direção do empuxo de propulsão
Um jato de água de seção transversal A e velocidade v1 atinge uma placa que se move com velocidade V. Determine a velocidade V, sabendo que A600m m 2 ,v 1 = 30m / seP =400N .
O bocal mostrado na figura descarrega água a uma vazão de 750 L /min. Sabendo que tanto em B como em C o jato de água se move com uma velocidade de intensidade de 30 m/s, e desprezando o peso do defle
Uma ferramenta rotativa é utilizada para remover a neve de uma seção em nível de uma linha férrea. O vagão removedor de neve é posicionado à frente de uma locomotiva que o empurra com uma velocidade c