Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Resistência dos Materiais- Ed: 5º - Capítulo 4.Problemas - Ex. 8
A junta é composta por três chapas de aço interligadas nas costuras. Determine o deslocamento da extremidade em relação à extremidade quando a junta for submetida às cargas axiais mostradas. Cada chapa tem espessura de .
Passo 1
O problema pede o deslocamento da extremidade em relação à extremidade vamos chamar esse valor de . Para isso a gente vai precisar aplicar a equação da deformação em função da força , comprimento inicial , área e coeficiente de elasticidade .
Características das chapas:
- Aço : . (Tabelado)
- Espessura: .
- Largura: .
Com isso a gente já pode achar a área e temos o coeficiente e o comprimento inicial . Falta apenas a força.
Passo 2
A sacada aqui é perceber que estamos lidando com três seções de áreas diferentes! Vamos calcular essas áreas então!
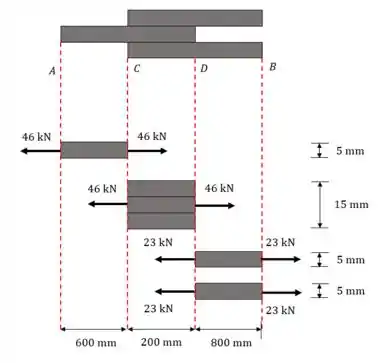
As forças na figura (fora de escala) você encontra pelo equilíbrio. O que nos importa aqui é calcular a área transversal pra cada seção. Lembre-se que a largura de todas é .
- Área da seção de a : .
- Área da seção de a : .
- Área de uma das seções de a : .
Moleza! Agora é só calcular a força!
Passo 3
As forças vão fazer o seguinte com a junta em cada seção:
- Puxar para esquerda, esticando .
- Puxar para esquerda e para direita, aumentando a seção toda um .
- Puxar para direita, esticando .
Então o movimento relativo de em relação a vai ser igual à soma do movimento de :
Lembrando que
Uma dica: Não precisa converter tudo para o S.I, pode usar . Aí o resultado aparece em :
Por fim:
Resposta
Deslocamento de em relação a : .