Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas - Ex. 82

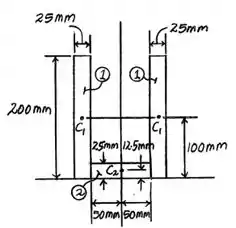
Localize o centroide y - da área da seção transversal da viga e depois determine os momentos de inércia dessa área e o produto de inércia em relação aos eixos u e v . Os eixos têm sua origem no centroide C .

Passo 1

O problema pede que encontremos o centroide y - e os momentos e produtos de inércia em relação aos eixos u e v .

Então, vamos começar calculando o centroide:

y - = ∑ y C ⋅ A ∑ A = 2 ⋅ 100 ⋅ 200 ⋅ 25 + 12,5 ⋅ 2,5 ⋅ ( 100 ) 2 ⋅ 200 ⋅ 25 + 25 ⋅ ( 100 )

y - = 82,5   m m

Passo 2

Agora, vamos calcular o momento e o produto de inércia com relação aos eixos x e y :

I x = 2 1 12 25 200 3 + 25 200 17,5 2 + 1 12 100 25 3 + 100 25 70 2

I x = 48,78 ⋅ 10 6   m m 4

Vamos para o eixo y agora:

I y = 2 1 12 200 25 3 + 200 25 62,5 2 + 1 12 25 100 3

I y = 41,67 ⋅ 10 6   m m 4

E usando a simetria no dividindo a figura no eixo y , temos que:

I x y = 0

Passo 3

E por fim, vamos calcular o momento e o produto de inércia com relação aos eixos u e v , pois já temos os I x ,   I y e   I x y :

I u = I x + I y 2 + I x - I y 2 ⋅ cos ⁡ 2 θ - I x y ⋅ s e n 2 θ

= 48,78 + 41,67 2 + 48,78 - 41,67 2 ⋅ cos ⁡ - 120 ° - 0 ⋅ s e n - 120 ° ⋅ 10 6

I u = 43,4 ⋅ 10 6   m m 4

Vamos para o eixo v :

I v = I x + I y 2 - I x - I y 2 ⋅ cos ⁡ 2 θ + I x y ⋅ s e n 2 θ

= 48,78 + 41,67 2 - 48,78 - 41,67 2 ⋅ cos ⁡ - 120 ° + 0 ⋅ s e n - 120 ° ⋅ 10 6

I v = 47 ⋅ 10 6   m m 4

E finalmente:

I u v = I x - I y 2 ⋅ s e n - 120 ° + 0 ⋅ c o s ⁡ ( - 120 ° )

I u v = - 3.08 ⋅ 10 6   m m 4

Resposta

y - = 82,5   m m

I u = 43,4 ⋅ 10 6   m m 4

I v = 47 ⋅ 10 6   m m 4

I u v = - 3.08 ⋅ 10 6   m m 4

Ver Outros Exercícios desse livro