Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 79

Localize o centroide y - da área da seção transversal da viga e depois determine os momentos de inércia e o produto de inércia dessa área em relação aos eixos u e v.

Passo 1

Figura: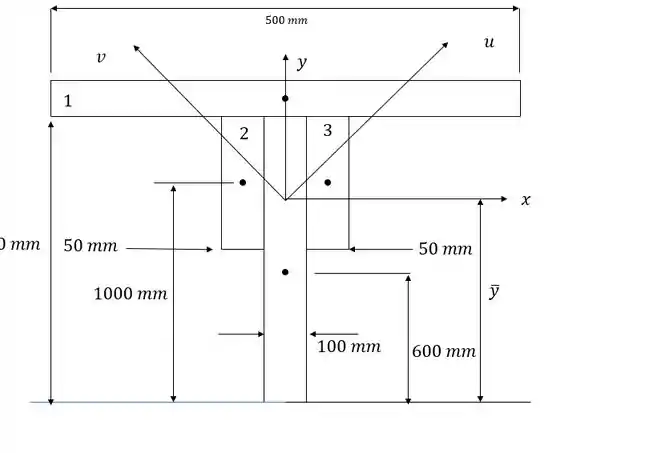

Passo 2

Podemos começar calculando a posição do centroide da composição, dividindo-a em três partes 1,2 e 3. O cálculo do centroide é dado por:

x - = ∑ d y A ∑ A y - = 1225 × 100 × 50 + 2 100 × 400 × 50 + 600 × 1200 × 100 100 × 50 + 2 × 400 × 50 + 1200 × 100 y - = 825   m m

Passo 3

Agora podemos calcular os momentos de inércia I x e I y :

I x = I x - + A d 2 I x = 1 12 × 1000 × 50 × 10 3 + 1000 × 50 × 400 2 + 2 × 1 12 × 50 × 400 3 + 0,5 × 400 × 175 2 + 1 12 × 100 × 1200 3 + 100 × 1200 × 225 2 I x = 302,44 × 10 8   m m 4

I y = I y - + A d 2 I y = 1 12 × 50 × 1000 3 + 2 × 1 12 × 400 × 50 3 + 4 × 50 × 75 2 + 1 12 × 1200 × 100 3 I y = 45 × 10 8   m m 4

Como a seção transversal é simétrica em relação ao eixo Y, então I x y = 0

Passo 4

Podemos calcular agora o momento de inércia em relação aos eixos pedidos:

I u = I x + I y 2 + I x - I y 2 c o s 2 θ - I x y s e n 2 θ θ = 60 º

I u = 302,44 × 10 8   m m 4 + 45 × 10 8   m m 4 2 + 302,44 × 10 8   m m 4 - 45 × 10 8   m m 4 2 c o s 2 × 60 - I x y s e n 2 × 60   I u = 109 × 10 8   m m 4

I v = I x + I y 2 - I x - I y 2 c o s 2 θ + I x y s e n 2 θ θ = 60 º

I v = 302,44 × 10 8   m m 4 + 45 × 10 8   m m 4 2 - 302,44 × 10 8   m m 4 - 45 × 10 8   m m 4 2 c o s 2 × 60 + I x y s e n 2 × 60   I v = 238 × 10 8   m m 4

I u v = I x - I y 2 s e n 2 × 60 + I x y c o s 2 × 60 I u v = 302,44 × 10 8   m m 4 - 45 × 10 8   m m 4 2 s e n 2 × 60 + 0 × s e n 2 × 60 I u v = 111 × 10 8   m m 4

Resposta

I u = 109 × 10 8   m m 4

I v = 238 × 10 8   m m 4

I u v = 111 × 10 8   m m 4

Ver Outros Exercícios desse livro