Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 6
Se uma força P = 25 N é aplicada à alça do mecanismo, determine a força que o parafuso exerce sobre a rolha da garrafa. O parafuso está conectado ao pino em A e passa pelo colar que está conectado à boca da garrafa em B.
Passo 1
Desenhando o diagrama do corpo livre e o diagrama de deslocamentos virtuais:
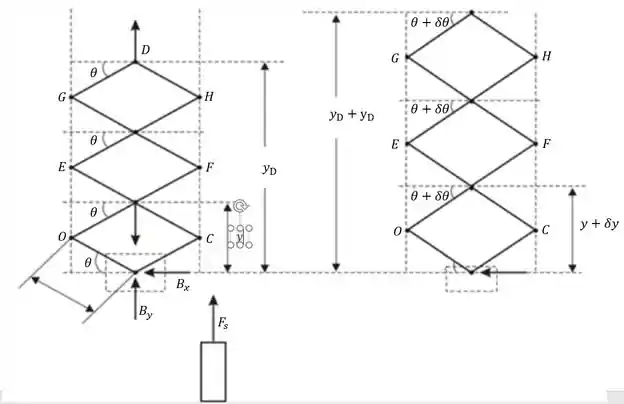
Passo 2
Como o comprimento de cada barra que forma o mecanismo é igual (BC=AC=AO ...), podemos escrever as coordenadas e em milímetros:
Analogamente para :
Passo 3
Achando os deslocamentos virtuais, derivando-se cada expressão temos:
Passo 4
Com todos os dados, podemos enfim calcular o trabalho virtual:
Passo 5
Substituindo os deslocamentos virtuais na expressão:
Como ≠0 :
Resposta
Exercícios de Livros Relacionados
A haste uniforme A B tem massa de 50k g . Se as duas molas D E e B C não estão deformadas quando θ = 90 ° , determine o ângulo θ para haver equilíbrio usando o princípio da energia potencial. Investig
A haste uniforme A B tem massa de 5k g . Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ de equilíbrio usando o método do trabalho virtual. Observe que a mola sempre perm
Os elementos uniformes A B e B C possuem massa de 1k g cada e o cilindro possui 10k g . Determine a força horizontal P necessária para manter o mecanismo em posição quando θ = 45 ° . A mola tem compri
Para o mecanismo mostrado, a mola de rigidez k tem um comprimento não alongado de essencialmente zero, e o elo maior tem uma massa m com centro de massa em B. A massa do elo menor é desprezível. Deter
Duas barras idênticas são soldadas em um ângulo de 120∘ e articuladas em O conforme mostrado. A massa da aba de suporte é pequena em comparação com a massa das barras. Investigue a estabilidade da pos