Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 76

Localize o centroide x - , y - da área da seção transversal da viga e depois determine o produto de inércia dessa área em relação aos eixos x ' e y ' .

Passo 1

Desenho:

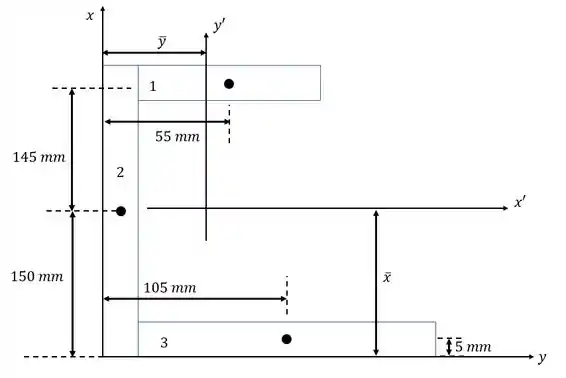
Passo 2

Escrevendo em uma tabela o tamanho de cada segmento do respectivo centro de massa:

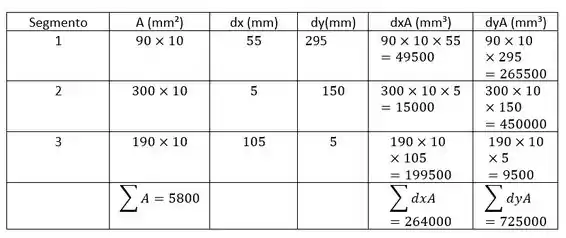
Passo 3

Calculando x -   e   y - :

x - = ∑ d x A ∑ A = 264 × 10 3 5,8 × 10 3 = 45,5   m m  

y - = ∑ d y A ∑ A = 725 × 10 3 5,8 × 10 3 = 125 m m  

Como os centroides de todos os segmentos são simétricos, então I x ' y ' = 0

Passo 4

Utilizando o teorema dos eixos paralelos para calcular o valor do momento de inércia em relação aos eixos pedidos:

I X ' Y ' = I X ' Y ' - + A d X ' d Y '

I X ' Y ' = 90 × 10 × 9,483 × 170 + 300 × 10 × - 40,52 × 25 + 190 × 10 × 59,48 × ( - 120 ) I X ' Y ' = - 15,15 × 10 6

Resposta

I X ' Y ' = - 15,15 × 10 6

Ver Outros Exercícios desse livro