Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 39
Se o coeficiente de atrito estático em B é , determine o maior ângulo e o menor coeficiente de atrito estático em A de modo que o cilindro permaneça preso, independente da intensidade da força P aplicada à correia. Despreze o peso do cilindro e o atrito entre a correia e a superfície vertical.
Passo 1
Desenhando o diagrama do corpo livre:
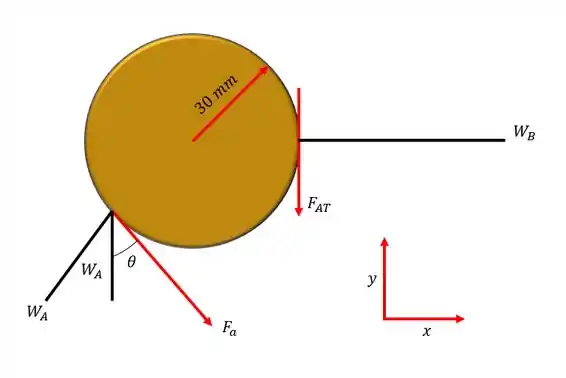
Passo 2
Podemos começar calculando a força de atrito em B:
Passo 3
Em seguida, pode-se calcular o equilíbrio em relação ao momento no ponto A:
Essa equação não tem solução analítica. Deve-se utilizar o método da tentativa e erro. Usando um software matemático, chegamos a:
Passo 4
Aplicando as equações do equilíbrio na direção x:
Passo 5
Aplicando as equações do equilíbrio na direção y:
Passo 6
Substituindo (1) em (2):
Resposta
Exercícios de Livros Relacionados
No Problema 8.43, determine o menor valor de θ para que a barra não caia fora do tubo.
Sabendo que θ = 45° , determine a faixa de valores de P para a qual o equilíbrio é mantido.
A engrenagem helicoidal de rosca quadrada mostrada tem um raio médio de 1,5p o l . E um avanço de 0,375p o l . A engrenagem grande é submetida a um par constante no sentido horário de 7,2k i p . i n .
Determine se o bloco mostrado está em equilíbrio e encontre a magnitude e a direção da força de atrito quando θ = 40° e P = 400N .
O bloco e o equipamento mostrados são usados para elevar uma carga de 150 lb. Cada uma das polias de 3 pol. De diâmetro gira em um eixo de 0,5 pol. Sabendo que o coeficiente de atrito estático é 0,20,