Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 9
Se uma força P=100 N for aplicada ao braço de alavanca da prensa articulada, determine a força de aperto desenvolvida no bloco quando . Despreze o peso do bloco.
Passo 1
Desenhando o diagrama do corpo livre:
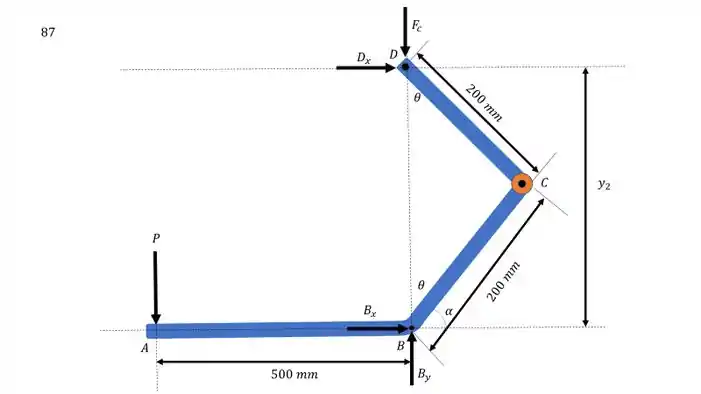
Passo 2
Desenhando o diagrama dos deslocamentos virtuais:
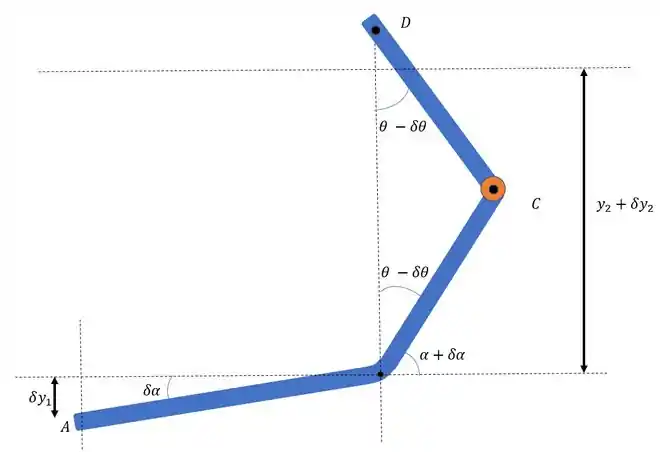
Passo 3
O primeiro passo é expressar as coordenadas de :
Passo 4
Para achar o deslocamento virtual, derivamos essa expressão em relação a :
Passo 5
Da segunda figura, temos que:
Como é um ângulo muito pequeno, podemos fazer a aproximação . Então:
Passo 6
Por fim, podemos utilizar a equação do deslocamento virtual:
Para acharmos uma relação entre e , podemos notar que . Derivando essa equação:
Substituindo na equação do deslocamento virtual:
Passo 7
Para :
Resposta
Exercícios de Livros Relacionados
Determine o valor de θ correspondente para a posição de equilíbrio do mecanismo do problema 10.11, quando P = 200N e Q = 720N .
Determine o valor de θ correspondente para a posição de equilíbrio do mecanismo do problema 10.9, quando P = 80N e Q = 100N .
A barra AB é fixada ao bloco A que desliza sem atrito na fenda vertical como mostrada na figura. Desprezando o efeito do atrito e o peso das barras, determine o valor de θ correspondente ao equilíbrio
Resolva o problema da 10.25 considerando que a força de 800N é substituída por um binário de 24N ⋅ m no sentido horário aplicado em D.
104- Os colares A e B são conectados por um arame A B e podem deslizar livremente nas barras sem atrito como mostra a figura. Sabendo que o comprimento do arame é 440m m e que o peso W do colar A é 90