Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 80
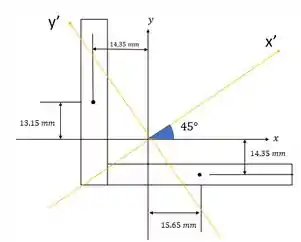
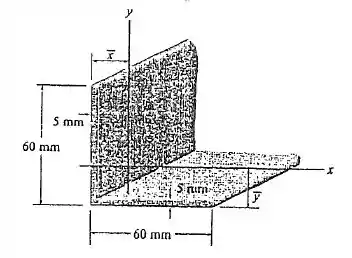
Localize os centroides e da área da seção transversal e depois determine a orientação dos eixos principais que têm sua origem no centroide C da área. Além disso, determine os momentos principais de inércia.
Passo 1
Cara, ele deu o passo a passo para a gente seguir. Mas repara que ele pede os eixos principais com origem no centroide. Para achar isso, a gente precisa achar os momentos de inércia e o produto de inércia em relação a eixos com origem nesse cara também.
Isso nos leva a usar dois sistemas de referência. O primeiro vai ser o para calcular o centroide. Aí a origem dele é num ponto de localização conhecida. E o segundo é para calcular os momentos de inércia. Esse tem origem no centroide.
Vamos começar achando o centroide dessa seção. Vamos dividir em figuras mais simples e calcular as coordenadas do centroide pela fórmulinha:
A gente vai dividir nossa figura assim:
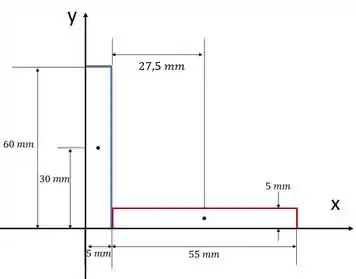
Repara que nossa primeiro sistema de referência tem origem ali na qui na da seção, onde a gente conhece a localização.
Passo 2
Podemos começar calculando o centroide. Nossas figuras são retângulos. O centroide de cada um é no centro de cada um. e são as coordenadas dos centroides das figuras mais simples em relação a e . E é a área de cada um.
Olhando a figura, nossas fórmulinhas ficam:
Passo 3
Calculando os momentos de inércia e o produto de inércia. Aqui a gente usa o novo sistema de referências, vamos chamar de novos e . A origem deles é no centroide que a gente acabou de calcular.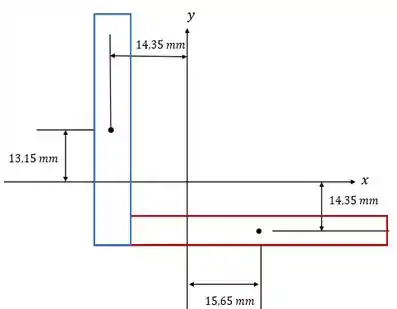
Para os momentos de inércia, a gente vai usar o teorema dos eixos paralelos. vai ser a distância do centroide de cada figura até o eixo , e ao eixo .A gente calculou eles e colocou na figura, pode reparar.
Aí partindo para os cálculos, vamos lembrar que no momento de inércia do retângulo a gente divide por o produto entre a dimensão do segmento paralelo ao eixo em questão e a dimensão do outro segmento elevada ao cubo. Ficamos assim:
Para o produto de inércia, a gente precisa usar o teorema dos eixos paralelos também, isso porque nosso centroide não coincide com os da figura. A gente faz:
Mas como os retângulos são figuras simétricas, todos eles tem . Daí a gente só precisa calcular:
Onde e são as coordenadas do centroide de cada figura em relação a esse novo sistema de coordenadas.
Passo 4
Após calculados os momentos de inércia e o produto de inércia, os momentos principais de inércia podem ser calculados pelas fórmulinhas:
Passo 5
A orientação dos eixos x e y podem ser calculadas pela expressão:
Isso quer dizer que os eixos principais de inércia fazem com os novos eixos e . Assim:
