Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 5
8.5. O homem de sobe pela escada e para na posição mostrada após sentir que a escada está na iminência do deslizamento. Determine a inclinação da escada se o coeficiente de atrito estático entre a plataforma de atrito A e o solo é . Assuma que a parede em B seja lisa. O centro de gravidade para o homem está em G. Despreze o peso da escada.
Passo 1
Vamos começar desenhando os diagramas de corpo livre.
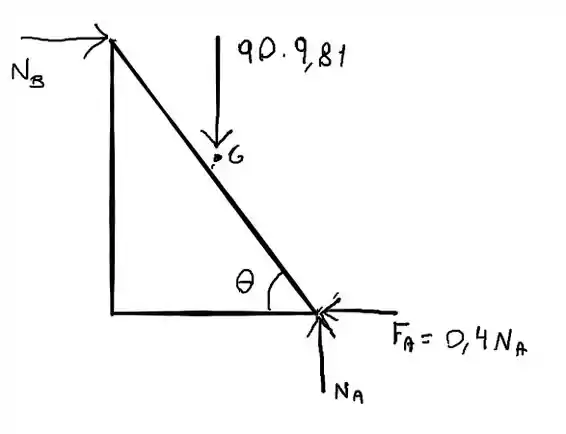
Passo 2
Agora vamos usar as equações de equilíbrio, para o primeiro caso temos
Então
Passo 3
Agora vamos usar a equação do momento no ponto B
Podemos dividir por e por
Isso nos dá
Resposta
Exercícios de Livros Relacionados
Determine a força P máxima que pode ser aplicada sem fazer com que as duas caixas de 50 k g se movam. O coeficiente de atrito estático entre cada caixa e o piso μ s = 0,25 .
Se P = 200 N , determine o atrito que se desenvolveu entre a caixa de 50 k g e o piso. O coeficiente de atrito estático entre a caixa e o piso é μ s = 0,3 .
Determine a força P mínima que pode ser aplicada sem causar o movimento da caixa de 125k g com centro de gravidade em G . O coeficiente de atrito estático no piso é μ s = 0,4 .
Determine a força P mínima para impedir que a barra A B de 30 k g deslize. A superfície de contato em B é lisa, enquanto o coeficiente de atrito estático entre a barra e a parede em A é μ s = 0,2 .
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0,5 , e