Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas de Revisão - Ex. 95b
Um macaco hidráulico pode ser usado para levantar o ponto B, de uma viga em balanço ABC. Sabendo-se que, depois da carga de 20kN ser aplicada, o ponto C deve estar no mesmo nível do ponto A, determinar:
- Quanto o Ponto B deve ser levantado;
- A reação em B, depois que B for levantado e a carga de 20kN for aplicada. Usar E=200GPa
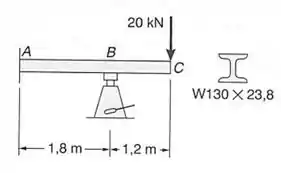
Passo 1
Então galera, vamos partir para a parte final do nosso capitulo, e para isso podemos ficar bem de boas, porque aqui vamos usar alguns conceitos bem interessantes, e para isso, podemos ver o seguinte.
Vamos supor que a nossa reação em B se chama , e a partir disso, vamos determinar os nossos diagramas de cada uma das cargas com relação ao ponto engastado. Fazendo isso, vamos ter que:
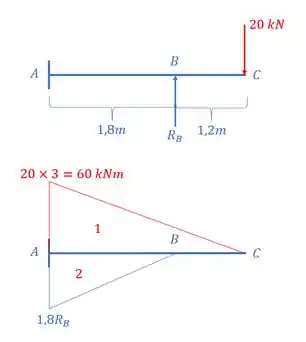
E aqui vai entrar um conceito novo bem importante, os nossos diagramas de momentos em si não podem nos ajudar diretamente, por isso é importante fazermos uma modificação nele, e é bem simples, como a inércia da nossa barra é toda igual pelo comprimento dela, basta dividirmos os diagramas por , mas se ela tivesse diferentes inércias em diferentes trechos, é só dividir cada trecho pelo seu respectivo, sendo assim o nosso diagrama passa a ser.
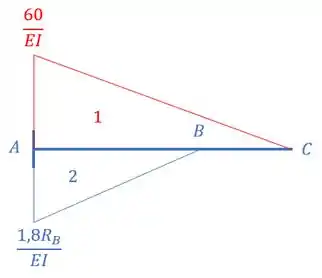
E é esse que vamos usar nos nossos cálculos, beleza?
Passo 2
Agora, ai invés da reação, vamos determinar a deformação do nosso ponto B, e para isso o principio vai ser bem simples.
Assim vamos ter que:
E se liga só, se o ponto A é um engaste, quanto é a deformação nele? Haha, olha que maravilha:
Então:
E como determinamos É bem tranquilo, lembra os diagramas que determinamos nos itens anteriores? Basta pegarmos a distancia do centroide de cada área, entre os pontos A e B, até o ponto em que queremos determinar o deslocamento (que nesse caso é o ponto B) e multiplicarmos pelas respectivas áreas e somar, muito tranquilo, né? Assim vamos ter que:
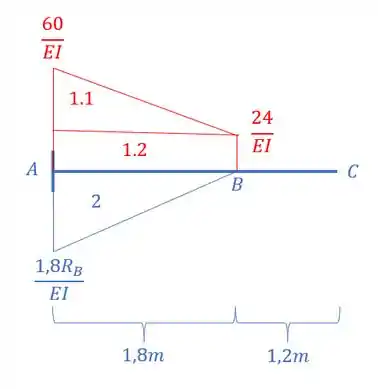
Determinando a distância do centroide até o termo que se quer a deformação, que nesse caso é o ponto B, obtém-se que:
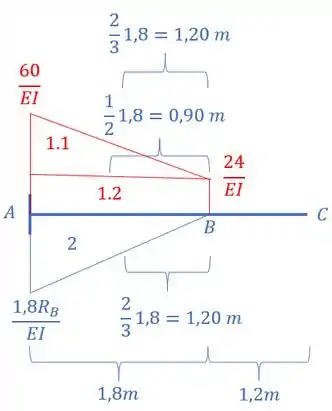
Sabe-se pelo item A) que , substituindo tem-se que:
Sabe-se que:
Substituindo, tem-se que: