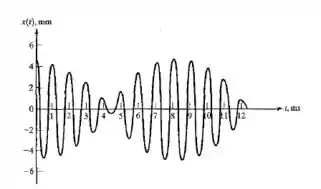
Uma máquina está sujeita a dois movimentos harmônicos, e o movimento resultante apresentado na tela de um osciloscópio é mostrado na figura 1.88. Determine as amplitudes e frequências dos dois movimentos.
Passo 1
Faaala amigos, prontos pra mais uma questãozinha? Bora!
Sabemos, por definição, que o movimento resultante de dois movimentos harmônicos com amplitudes iguais, mas frequências ligeiramente diferentes é dada pela seguinte equação Eq. (1.67):
Dito isso, sabemos que a máxima amplitude do movimento resultante é igual a e a frequência é igual a .
Passo 2
Da figura trazida no enunciado, encontramos que:
Ou seja, temos que:
Portanto:
Dessa conclusão, tiramos que a amplitude dos dois movimentos e as frequências dos mesmos, são .
Resposta
A amplitude de ambos os movimentos é e as frequências dos mesmos, são .