Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 95

Um momento M é aplicado à viga do problema 77, em torno do eixo z, causando zonas plásticas de 25 mm de espessura na parte superior e inferior da viga. Depois do momento ser removido determinar: (a) a tensão residual para y=50mm; (b) os pontos onde a tensão residual é nula; (c) o raio de curvatura correspondente à viga com a deformação permanente.

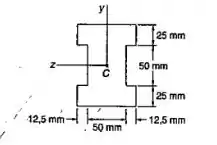
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos o eixo e dizermos qual deveria ser a tensãoresidual atuando no eixo. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser pegar os resultados obtidos lááááá no problema 77 e trazer tudo pra cá.

M = 51,6     k N . m

I = 5989583   m m 4

c = 50   m m

σ ' = 430,7   M P a

Para y=25mm, temos que :

σ ' = 215,35   M P a

σ r e s 1 =   - 300 + 215,35   =   - 84,65   M P a

Para y=50mm, temos que :

σ ' = 430,7   M P a

σ r e s 2 =   - 300 + 430,7 =   130,7   M P a

Para σ r e s = 0 :

y o = I σ r M

y o = 33,66   m m

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Para y=yr, temos que :

σ =   - E y ρ

ρ = 38,26   m  

Resposta

σ r e s 1 =   - 84,65   M P a

σ r e s 2 = 130,7   M P a

y o = 3 3,66   m m

ρ = 38,26   m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine ( a ) as equações das curvas de força cortante e momento fletor para a viga e o carregamento mostrados na figura e ( b ) o valor máximo absoluto do momento fletor na viga.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Usando o método da Seção 5.2 , resolva o Problema 5.20 .Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Determine ( a ) as equações das curvas de força cortante e momento fletor para a viga e o carregamento mostrados na figura e ( b ) o valor máximo absoluto do momento fletor na viga.