Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 51
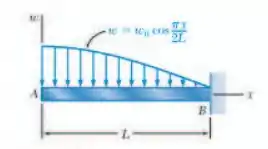
Determine as equações das curvas de força cortante e momento fletor para a viga e o carregamento mostrados na figura e o valor máximo absoluto do momento fletor na viga.
Passo 1
Fala aí gurizada, beleza? Bora resolver mais um exercício.
Para encontrarmos os diagramas de força cortante e momento fletor pedidos, precisamos utilizar uma relação que nos diz que a inclinação de uma viga carregada, dada por , da curva da força cortante é negativa e a intensidade da inclinação em qualquer ponto é igual à força por unidade de comprimento naquele ponto, portanto:
Substituindo a carga distribuída , temos:
Para encontrarmos a constante , temos que substituir a seguinte condição de contorno:
Substituindo:
Com isso, nossa equação para a curva da força cortante vai ser:
Agora que encontramos a equação para a força cortante, bora encontrar a equação para o momento fletor.
Passo 2
Para isso, devemos integrar a equação para a força cortante que encontramos no passo anterior. Fica assim:
Agora, galera, vamos utilizar a seguinte condição de contorno para encontrarmos a nossa constante :
Logo:
Com a constante encontrada, a equação para o momento fletor vai ser dada por:
Agora a gente precisa determinar o momento máximo absoluto, para isso, precisamos determinar um ponto tal que tenhamos o valor máximo. Neste caso, o valor máximo para o momento fletor ocorre em . Subsituindo na equação que a gente encontrou:
Isso é tudo, pessoal!!!