Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 103

Os momentos de inércia e o produto de inércia de uma seção transversal da cantoneira de L 102 × 76 × 6,4   m m em relação a dois eixos retangulares x e y passando por C são, respectivamente, I x = 0,166 × 10 6   m m 4 , I y = 0,453 × 10 6   m m 4 e I x y < 0 , sendo I m í n = 0,051 × 10 6   m m 4 o valor mínimo do momento de inércia da superfície em relação a qualquer eixo que passa por C . Usando o círculo de Mohr, determine a o produto de inércia I x y da superfície, b a orientação dos eixos principais, c o valor de I m á x .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte círculo de Mohr:

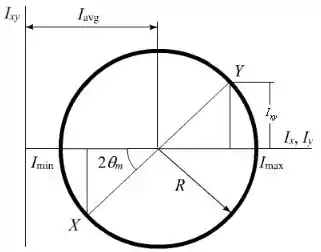
O centro do círculo de Mohr está localizado a uma distância I m é d da origem. Portanto:

I m é d = 1 2 I x + I y

I m é d = 1 2 0,166 × 10 6 + 0,453 × 10 6

I m é d = 0,3095 × 10 6   m m 4

Passo 2

Sabemos que:

I m í n = I m é d - R

Portanto:

R = I m é d - I m í n

R = 0,2585 × 10 6   m m 4

Sabemos também que o raio R do círculo de Mohr é dado por:

R = I x - I y 2 2 + I x y 2

Logo, podemos dizer que:

R 2 = I x - I y 2 2 + I x y 2

I x y = R 2 - I x - I y 2 2

Logo:

I x y = 0,2585 × 10 6 2 - 0,166 × 10 6 - 0,453 × 10 6 2 2

I x y = ± 0,2150 × 10 6   m m 4

Como nos é dito que:

I x y < 0

Temos que:

I x y = - 0,2150 × 10 6   m m 4

Passo 3

Usando o círculo de Mohr, podemos encontrar θ m a partir de:

tan ⁡ 2 θ m = - 2 I x y I x - I y

tan ⁡ 2 θ m = - 2 - 0,2150 × 10 6 0,166 × 10 6 - 0,453 × 10 6

2 θ m = - 56,28 °

E:

θ m = - 28,1 °

Passo 4

Usando o círculo de Mohr, podemos então determinar o valor de I m á x :

I m á x = I m é d + R

I m á x = 0,3095 × 10 6 + 0,2585 × 10 6

Logo:

I m á x = 0,568 × 10 6   m m 4

Resposta

a )   I x y = - 0,2150 × 10 6   m m 4

b )   θ m = - 28,1 °  

c )   I m á x = 0,568 × 10 6   m m 4

Ver Outros Exercícios desse livro