Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 88
A montegem é feita de um hemisfério de aço, e um cilindro de aluminio, . Determine a altura do cilindro de modo que o centro de massa da montagem esteja localizada em .
Passo 1
O problema quer que a gente encontre para que , levando em conta as densidades e , pra isso vamos usar a massa do hemisfério e a massa do cilindro . Sabemos que o é dado por na questão por:
Passo 2
Primeiro gente vai pegar os valores tabelados do centro de massa de um hemisfério e de um cilindro, você pode achar eles na internet, mas também fica no final do livro, nele a gente encontra que o centro de massa do:
Confere lá no final do livro, mas se precisar de ajuda tem umas vídeo aulas bem legais aqui mesmo no Responde aí.
Agora, vamos calcular os na estrutura do problema:
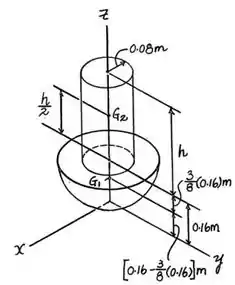
Passo 3
Agora, vamos calcular o volume do hemisfério e o do cilindro, também pode ser encontrado no final do livro, então, vamos lá:
Lembra daquela densidade que a questão deu? Vamos usar agora para calcular as massas:
Obs.: Não precisa se preocupar com a unidade de massa nesse caso, que não influencia no nosso resultado, por causa da divisão pela mesma univade.
Então, agora vamos usar a formula do centróide resultante, pois já sabemos que :
Agora resolvendo essa equação, encontramos que: