Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 75

Determine a distância x - até o centroide do sólido que consiste em um cilindro com um furo de profundidade h   =   50   m m escavado em sua base.

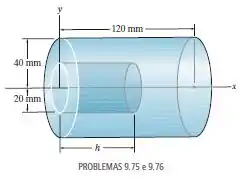
Passo 1

Oi tudo bem? Vamos resolver este exercício.

Queremos a massa e a localização ( x - ,   y - ,   z - ) do centro de massa G desta placa composta de aço e latão.

Para o cálculo da massa, temos que:

m = ρ ⋅ V

O volume da placa é igual ao produto do comprimento, largura e espessura do elemento.

Vamos dividir o elemento da seguinte maneira:

A massa da parte 1 será:

m 1 = 7,85   M g / m 3 1000 k g M g ⋅ 150 ⋅ 10 - 3   m 225 ⋅ 10 - 3   m 30 ⋅ 10 - 3   m

m 1 = 7,85 ⋅ 10 3 ⋅ 0,15 ⋅ 0,225 ⋅ 0,3

m 1 = 7,95   k g

A massa da parte 2 será:

m 2 = 7,85   M g / m 3 1000 k g M g ⋅ 1 2 150 ⋅ 10 - 3   m 225 ⋅ 10 - 3   m 30 ⋅ 10 - 3   m

m 2 = 7,85 ⋅ 10 3 ⋅ 1 2 ⋅ 0,15 ⋅ 0,225 ⋅ 0,3

m 2 = 3,975   k g

A massa da parte 3 será:

m 3 = 8,74   M g / m 3 1000 k g M g ⋅ 1 2 150 ⋅ 10 - 3   m 225 ⋅ 10 - 3   m 30 ⋅ 10 - 3   m

m 3 = 8,74 ⋅ 10 3 ⋅ 1 2 ⋅ 0,15 ⋅ 0,225 ⋅ 0,3

m 3 = 4,425   k g

Passo 2

A localização do centroide do elemento 1 com relação a x será:

x 1 = 0,150 2

x 1 = 0,075   m

A localização do centroide do elemento 2 com relação a x será:

x 2 = 0,15 3 + 0,15

x 2 = 0,2   m

A localização do centroide do elemento 3 com relação a x será:

x 3 = 0,15 2 3 + 0,15

x 1 = 0,25   m

Passo 3

A localização do centroide do elemento 1 com relação a z será:

z 1 = 0,225 2

z 1 = 0,1125   m

A localização do centroide do elemento 2 com relação a z será:

z 2 = 2 3 ( 0,225 )

z 2 = 0,15   m

A localização do centroide do elemento 3 com relação a x será:

z 3 = 1 3 0,225

z 1 = 0,075   m

Passo 4

De posse destes dados podemos encontrar o centroide do elemento inteiro, bem como sua massa total.

Temos que:

M = ∑ m i

Logo:

M = m 1 + m 2 + m 3

M = 7,95 + 3,975 + 4,425

M = 16,35   k g

O centro de massa da placa composta em torno de x será:

x - = ∑ x i m i ∑ m i

x - = 0,075 7,95 + 0,2 3,975 + 0,25 4,425 16,35

x - = 0,15275   m

O centro de massa da placa composta em torno de y será:

y - = - 1 2 30 ⋅ 10 - 3

y - = - 0,015   m

O centro de massa da placa composta em torno de z será:

z - = ∑ z i m i ∑ m i

z - = 0,1125 7,95 + 0,15 3,975 + 0,075 4,425 16,35

z - = 0,11145   m

Resposta

x - = 0,15275   m

y - = - 0,015   m

z - = 0,11145   m

M = 16,35   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as reações de apoio em A e B para a viga submetida às duas cargas distribuídas linearmente.
A carga por pé de comprimento da viga varia conforme mostrado. Para x = 10 pés, a carga unitária é w = 300 lb / pés. Em x = 0, a carga está aumentando a uma taxa de 50 lb / pés por pé. Calcule as reaç
Desenhe os diagramas de cisalhamento e momento para a viga carregada. Quais são os valores de cisalhamento e momento na viga média?
Desenhe os diagramas de cisalhamento e momento para a viga cantilever carregada. Indique o valor do momento fletor na viga média.
Desenhe os diagramas de cortante e momento para a viga carregada e determine a distância d à direita de A onde o momento é zero.