Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 128

Demonstre que as Eqs. ( 8.13 ) e ( 8.14 ) são válidas para qualquer formato de superfície, desde que o coeficiente de atrito seja o mesmo em todos os pontos de contato.

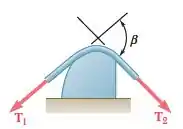
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte diagrama de corpo livre da superfície:

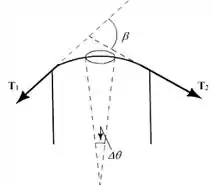
Vamos agora pegar uma parte dessa superfície e analisar:

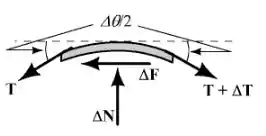
Temos que:

∑ F y = 0

∆ N - T + T + ∆ T sen ⁡ ∆ θ 2 = 0

∆ N = 2 T + ∆ T sen ⁡ ∆ θ 2

Passo 2

O somatório das forças em x nos dá:

∑ F x = 0

T + ∆ T - T cos ⁡ ∆ θ 2 - ∆ F = 0

Logo:

∆ F = ∆ T cos ⁡ ∆ θ 2

Quando houver escorregamento iminente, temos que:

∆ F = μ s ∆ N

Logo:

∆ T cos ⁡ ∆ θ 2 = μ s 2 T + ∆ T sen ⁡ ∆ θ 2

Dividindo os dois lados por ∆ θ , temos que:

∆ T ∆ θ cos ⁡ ∆ θ 2 = μ s 2 T + ∆ T ∆ θ sen ⁡ ∆ θ 2

Passo 3

Podemos então aplicar o limite ∆ θ → 0 e resolver:

Temos que:

d T d θ = μ s T

d T T = μ s d θ

Intefrando, temos que:

∫ T 1 T 2 d T T = ∫ 0 β μ s d θ

ln ⁡ T 2 T 1 = μ s β

Logo:

T 2 T 1 = e μ s β

Provando assim que:

ln ⁡ T 2 T 1 = μ s β

E:

T 2 T 1 = e μ s β

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

111. Resolva o problema 8.110 , considerando que o tambor A está girando em sentido anti-horário
112. Um freio de cinta é utilizado para controlar a velocidade de um volante, conforme mostra a figura. Os coeficientes de atrito são μ s = 0,30 e μ k = 0,25 . Determine a intensidade do torque que de
Se θ = 30 ° , determine o menor coeficiente de atrito estático em A e B de modo que o equilíbrio da estrutura de suporte seja mantido, independentemente da massa do cilindro. Desconsidere a massa das
Determine a força horizontal P máxima que pode ser aplicada à argola de 12k g sem fazer com que ela gire. O coeficiente de atrito estático entre a argola e as superfícies em A e B é μ s = 0,2 . Consid
Se o coeficiente de atrito estático em A e B é μ s = 0,6 , determine o ângulo máximo θ para o sistema permanecer em equilíbrio, independentemente da massa do cilindro. Desconsidere a massa das hastes.