Um motor de avião tem uma massa desbalanceada em rotação no raio . Se a asa puder ser modelada como uma viga em balanço de seção transversal uniforme , como mostra a Figura 3.34(b), determine a deflexão máxima do motor a uma velocidade de rpm. Admita que o amortecimento e o efeito da asa entre o motor e a extremidade livre são desprezíveis.

Rigidez equivalente da asa (viga) na localização do motor

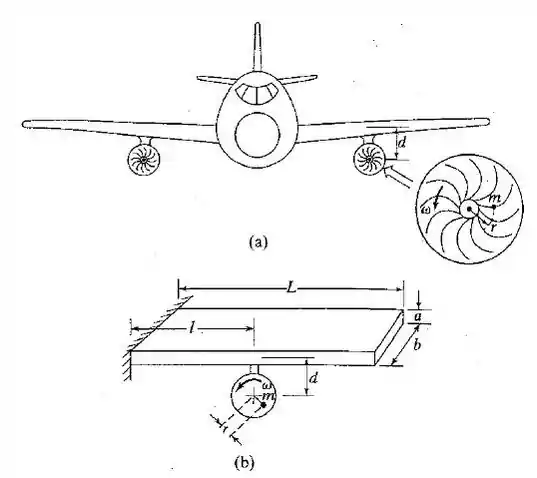
Magnitude da força desbalanceada

Massa equivalente da asa na localização do motor: :

Equação do movimento :

Deslocamento máximo em estado estacionário da asa na localização do motor: