O motor tem uma massa de 25 kg e um raio de giração de 0,06 m em relação ao eixo z. O eixo do motor está suportado por mancais em A e B, e rotaciona a uma taxa constante , enquanto a estrutura tem uma velocidade angular . Determine o momento que as forças dos mancais em A e B exercem sobre o eixo em virtude desse movimento.
Passo 1
Começaremos o exercício aplicando a equação 21-30 apresentada no livro para o sistema de coordenadas mostrado no diagrama a seguir:
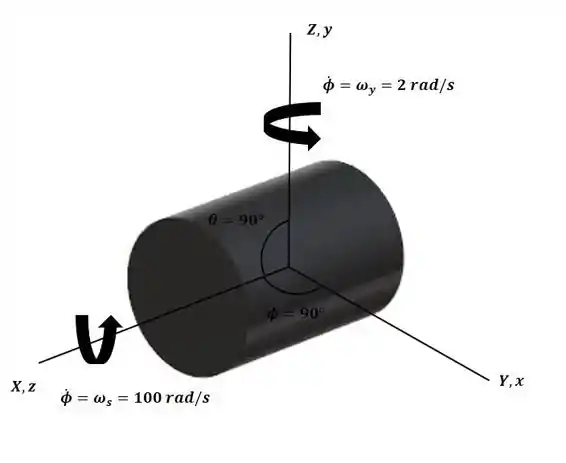
Passo 2
Como não temos velocidade angular em x, logo:
E consequentemente: