Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 38

O pacote de 40   k g é jogado a uma velocidade de 4   m / s sobre o carrinho, que tem massa de 20   k g . Se o pacote desliza sobre a superfície lisa e atinge a mola, determine a velocidade do carrinho no instante em que o pacote comprime totalmente a mola. Qual é a compressão máxima da mola? Despreze a resistência ao rolamento do carrinho.

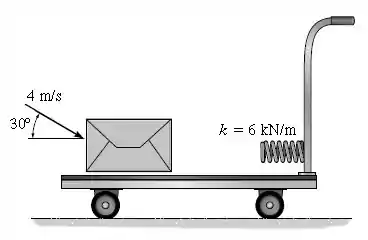
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar conservação de quantidade de movimento para encontrar a velocidade do pacote após a colisão:

→ +         ∑ m v 1 = ∑ m v 2

→ +         m p v p 1 x + m c v c 1 = m p v p 2 x + m c v c 2

Substituindo os valores, temos:

→ +         40 4 cos ⁡ 30 ° + 0 = 40 v p 2 + 0

v p 2 = 3,464   m / s     →

Passo 2

Quando a mola é totalmente comprimida, temos:

→ +         m p v p 2 + m c v c 2 = m p + m c v 3

40 3,464 + 0 = 40 + 20 v 3

v 3 = 2,31   m / s

Passo 3

Aplicando conservação de energia, temos:

T 2 + V 2 = T 3 + V 3

1 2 m p v p 2 2 + 1 2 m c v c 2 2 + V e 2 = 1 2 m p + m c v 3 2 + V e 3

1 2 40 3,464 2 + 0 + 0 = 1 2 40 + 20 ( 2,31 ) 2 + 3000 s m á x 2

s M á x = 0,163   m

Resposta

v 3 = 2,31   m / s

s M á x = 0,163   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

130. O segundo estágio B do foguete de dois estágios tem uma massa de 5Mg (vazio) e é lançado a partir do primeiro estágio A com uma velocidade inicial de 600 Km/h. O combustível do segundo estágio te
133. O caminhão tem massa de 50Mg quando está vazio. Quando está descarregado 5 m 3 de areia a uma taxa constante de 0,8 m 3 s , a areia flui para fora a uma velocidade de 7m/s, medida em relação ao c
138. O vagão é usado para coletar água acumulada em uma calha nos trilhos. Determine a forca necessária para impelir o vagão a uma velocidade constanve v, para cada um dos três casos. O coletor tem um
126. Um limpa-trilhos localizado na frente de uma locomotiva junta neve a uma taxa de 0,27 m 3 / s e a armazena no trem. Se a locomotiva está viajando a uma velocidade constante de 3,6 m/s, determine
127. O barco tem uma massa de 180kg e está viajando por um rio a uma velocidade constante de 70km/h, medida em relação ao rio. O rio está fluindo na direção oposta a 5km/h. Se um tubo é colocado na ág