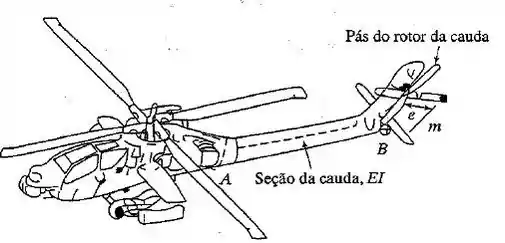
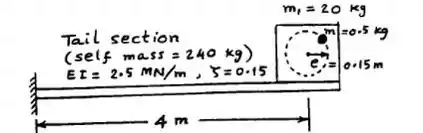
Uma das pás do rotor da cauda de um helicóptero tem uma massa desbalanceada de a uma distâneia do eixo de rotaçāo, como mostra a Figura . A seção da cauda tem comprimento de , massa de , rigidez à flexão de e fator de amortecimento de 0,15 . A massa das pás do rotor traseiro, incluindo seu sistema de acionamento, é . Determine a resposta forçada da seção da cauda quando as pás giram a .

mola constante de viga cantilever

Resposta forçada é dada

Em que