Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 53

As pás de uma turbina de vento giram em torno do mancal S com uma velocidade angular constante de ω S , enquanto a estrutura realiza uma precessão em torno do eixo vertical com uma velocidade angular constante de ω p . Determmine as componentes x , y , z do momento que o mancal exerce sobre as pás como uma função de θ . Considere cada pá como uma barra fina de massa m e comprimento l .

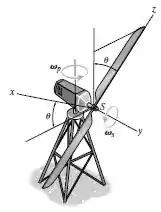
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Ao rotacionar a cabeça, a angulação irá gerar componentes da velocidade angular ω p . São elas:

ω p = ω p sin ⁡ θ i + ω p cos ⁡ θ k

Do enunciado, temos que ω S , portanto, o vetor velocidade resultante do sistema neste momento é:

ω = ω p + ω S

ω = ω p sin ⁡ θ i + ω p cos ⁡ θ k + ω S j

A aceleração angular da cabeça ω ˙ com relação ao eixo x y z pode ser obtida considerando um novo eixo x ' y ' z ' que tem uma velocidade angular de Ω ' = ω p = ω p sin ⁡ θ i + ω p cos ⁡ θ k . Portanto:

ω ˙ = ω ˙ x ' y ' z ' + Ω ' × ω

Podemos dividir da seguinte forma:

ω ˙ = ω ˙ 1 x ' y ' z ' + ω ˙ 2 x ' y ' z ' + Ω ' × ω 1 + Ω ' × ω 2

ω ˙ = 0 + 0 + ω p sin ⁡ θ i + ω p cos ⁡ θ k × ω s j + 0

ω ˙ = ω p ω s sin ⁡ θ k - ω p ω s cos ⁡ θ i

As componentes são dadas por:

ω ˙ x = - ω p ω s cos ⁡ θ

ω ˙ y = 0

ω ˙ z = ω p ω s sin ⁡ θ

Os momentos de inércia são dados por:

I x = I y = 1 12 2 m 2 l 2

I z = 0

I x = I y = 2 3 m l 2

Agora temos todos os dados necessários para calcular as componentes do momento. Elas são dadas por:

∑ M x = I x ω ˙ x - I y - I z ω y ω z

M x = 2 3 m l 2 - ω p ω s cos ⁡ θ - 2 3 m l 2 - 0 ( ω S ) ( ω p cos ⁡ θ )

M x = - 4 3 m l 2 ω s ω p cos ⁡ θ

∑ M y = I y ω ˙ y - I z - I x ω x ω z

M y = 0 - 0 - 2 3 m l 2 ω p cos ⁡ θ ω p sin ⁡ θ

M y = 1 3 m l 2 ω p 2 sin ⁡ 2 θ

∑ M z = I z ω ˙ z - I x - I y ω x ω y

M z = 0 - 0

M z = 0

Resposta

M x = - 4 3 m l 2 ω s ω p cos ⁡ θ

M y = 1 3 m l 2 ω p 2 sin ⁡ 2 θ

M z = 0

Ver Outros Exercícios desse livro