Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 194

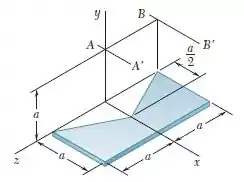
Um pedaço de chapa metálica delgada e uniforme é cortado para formar o componente de máquina mostrado na figura. Representada a massa de componente por m , determine seu momento de inércia de massa em relação a ao eixo A A ' , b ao eixo B B ' , sendo os eixos A A ' e B B ' paralelos ao eixo x e pertencentes ao plano paralelo ao plano x z a uma distância a acima.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Sabemos que m = ρ V .

m = ρ t A

m = ρ t 2 a a - 1 2 2 a a 2

m = 3 2 ρ t a 2

Podemos organizar da seguinte forma:

ρ t = 2 m 3 a 2

Sabemos também que o momento de inércia de massa é dado por:

I m a s s a = ρ t I á r e a

Logo:

I m a s s a = 2 m 3 a 2 I á r e a

Passo 2

Da figura do enunciado, temos que:

I x = I x 1 - I x 2 - I x 3

Substituindo, temos que:

I x = 1 12 a 2 a 3 - 1 12 a 2 a 3 - 1 12 a 2 a 3

I x = 7 12 a 4

Logo:

I x m a s s a = 2 m 3 a 2 I x

I x m a s s a = 2 m 3 a 2 7 12 a 4

I x m a s s a = 7 18 m a 2

Temos que:

I = I x m a s s a + m d 2

Logo:

I A A ' = 7 18 m a 2 + m a 2

I A A ' = 1,389 m a 2

Passo 3

Item b:

O momento de inércia de massa em relação ao eixo B B ' é dado por:

I B B ' = I x m a s s a + m a 2 2

I B B ' = 7 18 m a 2 + 2 m a 2

I B B ' = 2,389 m a 2

Resposta

a )   I A A ' = 1,389 m a 2

b ) I B B ' = 2,389 m a 2

Ver Outros Exercícios desse livro