Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 168

Um pedaço de chapa metálica de espessura t e massa específica γ é cortada e dobrada no formato mostrado na figura. Determine seu momento de inércia de massa em relação à linha que liga a origem O e ponto A .

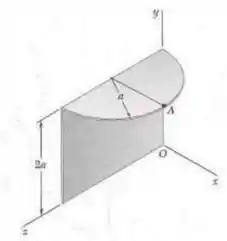
Passo 1

Primeiramente devemos notar que

λ O A = 1 6 ⋅ i + 2 j + k

Considerando que nossa chapa é composta de 2 partes (o semi-círculo e o quadrado) temos que calcular a massa de cada uma dessas partes que vão ser dadas por

m 1 = γ g ⋅ t ⋅ 4 a 2

m 2 = γ g ⋅ t ⋅ π 2 ⋅ a 2

Utilizando a imagem presente do livro que diz

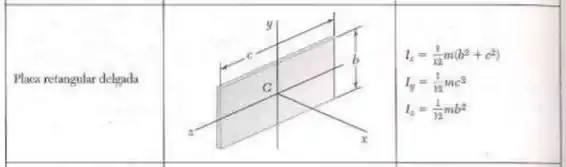
Além disso, temos que

I x = I x 1 + I x 2

I x = 1 12 ⋅ 4 γ t a 4 g ⋅ 8 a 2 + 8 γ t a 4 g + 1 4 ⋅ π 2 ⋅ γ t a 4 g + π 2 ⋅ γ t g ⋅ 5 a 4 ≈ 18.91335 ⋅ γ t a 4 g

Fazendo o mesmo agora para I y teremos

I y = 1 12 ⋅ 4 γ t a 2 g ⋅ 4 a 2 + 4 γ t a 4 g + π 2 ⋅ γ t g ⋅ a 2 ⋅ 1 2 - 16 9 π 2 ⋅ a 2 + π 2 ⋅ γ t g ⋅ a 2 ⋅ 4 a 3 π 2 + a 2

I y ≈ 7.68953 ⋅ γ t a 4 g  

Por fim, fazendo o mesmo para I z vamos obter

I z = 1 12 ⋅ 4 γ t a 2 g ⋅ 4 a 2 + 4 γ t a 4 g + π 2 ⋅ γ t g ⋅ a 2 ⋅ 1 4 - 16 9 π 2 ⋅ a 2 + π 2 ⋅ γ t g ⋅ a 2 ⋅ 4 a 3 π 2 + 4 a 2

I z ≈ 12 ⋅ γ t a 4 g

Devido a simetria temos que os produtos de inércia I x ' y ' - ,     I y ' z ' -   e   I z ' x ' - são iguais a zero e além disso, x 1 - = 0 . Então,

I x y = ∑ I x ' y ' - + m x - y - = m 2 ⋅ x 2 - ⋅ y 2 - = π 2 ⋅ γ t a 4 3 π ⋅ g ⋅ 8 = 4 3 ⋅ γ t a 4 g

I y z = ∑ I y ' z ' - + m z - y - = m 1 ⋅ x 1 - ⋅ y 1 - + m 2 ⋅ x 2 - ⋅ y 2 - = 4 γ t a 4 g + π γ t a 4 g ≈ 7.14159 ⋅ γ t a 4 g

I z x = ∑ I x ' z ' - + m z - x - = m 2 ⋅ z 2 - ⋅ x 2 - = 2 3 ⋅ π γ t a 4 g

Passo 2

Assim a equação que vai nos fornecer o momento de inércia desejado é dada por

I o a = I x ⋅ λ x 2 + I y ⋅ λ y 2 + I z ⋅ λ z 2 - 2 I x y ⋅ λ x ⋅ λ y - 2 I y z ⋅ λ y ⋅ λ z - 2 I z x ⋅ λ z ⋅ λ x

Substituindo os valores encontrados acima vamos obter

I O A = 3.15223 + 5.12635 + 2.00154 - 0.88889 - 4.76106 - 0.22222 ⋅ γ t a 4 g ≈ 4.41 ⋅ γ t a 4 g

Resposta

I O A = 4.41 ⋅ γ t a 4 g

Ver Outros Exercícios desse livro