Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 173
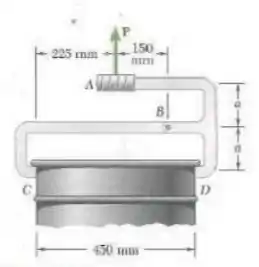
Um pequeno barril com peso de é erguido por um par de garras tal como mostra a figura. Sabendo que , determine as forças exercidas em e na garra .
Passo 1
Primeiramente devemos notar que é um membro de duas forças. Sendo assim, podemos estabelecer a seguinte proporção entre as forças em
Aplicando, agora, as condições de equilíbrio vamos ter
Como vamos ter
Passo 2
Continuando aplicando as condições de equilíbrio vamos ter
Por fim, encontramos
Resposta
Exercícios de Livros Relacionados
As dimensões de um guindaste, que é fabricado pela Basick Co., são dadas na figura. Se o guindaste tem massa de 800 kg e centro de massa em G . O mancal em A é radial e apoia somente uma força horizon
Uma tira de metal rígida, com peso desprezível, é usada como parte da chave eletromagnética. Determine a rigidez máxima das molas em A e B de modo que o contato em C seja fechado quando a força vertic
Se a corda B C se romper quando a tração tornar-se 50 kN, determine a maior carga vertical F que pode ser aplicada à viga em B . Qual é a intensidade da reação em A para esse carregamento? Desconsider
A haste uniforme de 10 kg tem um pino na extremidade A . Se ela também estiver sujeita a um momento de binário de 50N ⋅ m , determine o menor ângulo θ para o equilíbrio. A mola não está esticada quand
O atuador pneumático em D é usado para aplicar uma força de F = 200N sobre o membro em B . Determine as componentes horizontal e vertical da reação no pino A e a força do eixo liso em C sobre o membro