Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas - Ex. 106

O pêndulo consiste em um disco de massa 6   k g e barras esbeltas A B e D C , que têm massa por unidade de comprimento de 2   k g / m . Determine o comprimento L de D C de modo que o centro de massa esteja no apoio O . Qual é o momento de inércia do conjunto em relação ao eixo perpendicular à página e que passa pelo ponto O ?

Passo 1

O problema pede que encontremos o momento de inércia do conjunto em um eixo perpendicular à página e que passe pelo ponto O .

Vamos usar a formula do centroide, porque na questão já notamos o ponto O , como centroide:

x - = ∑ x - m ∑ m

0,5 = 1,5 6 + 0,65 1,3 2 + 0 [ L ( 2 ) ] 6 + 1,3 2 + L ( 2 )

L = 6,39   m

Passo 2

Agora, vamos observar que os momentos de inércia podem ser dados por:

I G B a r r a = 1 12 m B l 2

I G E s f e r a = 2 5 m E r 2

Passo 3

E finalmente calculando o momento de inercia com as informações que temos, em relação ao ponto O , fica:

I O = ∑ ( I G + m d 2 )

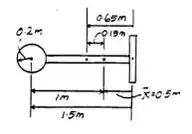
Então:

I O = 1 12 1,3 2 ( 1,3 2 ) + [ 1,3 ( 2 ) ] ( 0,15 2 )

Calculando isso, temos:

I O = 53,2   k g ⋅ m 2

Resposta

L = 6,39   m

I O = 53,2   k g ⋅ m 2

Ver Outros Exercícios desse livro