Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 72
O pião de 0,5 kg tem um centro de gravidade no ponto G. Se ele rotaciona em torno de seu eixo de simetria e realiza uma precessão em torno do eixo vertical a taxas constantes e , respectivamente, determine o ângulo em regime estacionário. O raio de giração do pião em relação ao eixo z é , e em relação aos eixos x e y é .
Passo 1
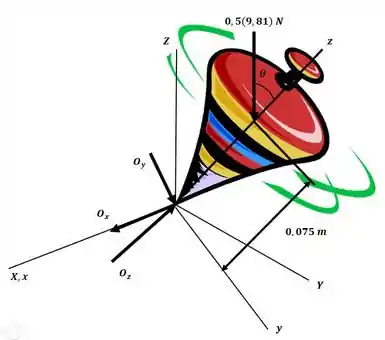
Uma vez que e e são constantes, o pião está sob precessão estacionária conforme ilustrado na figura a seguir:
Passo 2
Sendo assim, podemos agora calcular o momento de inércia do sistema em relação aos eixos principais:
Passo 3
Sendo assim, podemos aplicar a equação de momento com relação ao eixo x:
Resolvendo para :