O pião tem uma massa de 90 g, um centro de massa em G e um raio de giração k = 18 mm em relação a seu eixo de simetria. Em torno de qualquer eixo transversal atuando através do ponto O, o raio de giração é . Se o pião está conectado a uma junta esférica em O e a precessão é , determine a rotação .
Passo 1
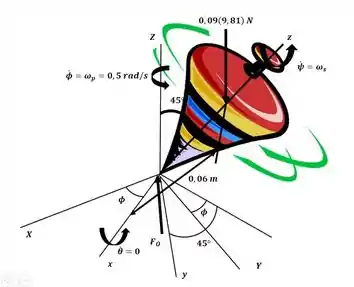
Começaremos o exercício analisando a figura a seguir para poder aplicar a equação de momento apresentada no capítulo para o eixo x:
Passo 2
Agora podemos aplicar a equação de momento para o sistema:
Resolvendo para :