Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 36

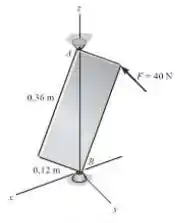
A placa de 7,5   k g está sujeita a uma força F = 40   N que é sempre perpendicular à face da placa. Se a placa está originalmente em repouso, determine sua velocidade angular após ela ter girado uma revolução ( 360 ° ) . A placa é suportada pelas juntas esféricas A e B .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Por definição, temos que:

H O 1 + ∑ ∫ M O d t = H O 2

Aplicando ao problema, temos que:

0 + r A / O × I s = H O 2

0 + - 0,2 0,7071 j - 0,2 0,7071 k × - 60 i = I O x ω x i + I O y ω y j + I O z ω z k

Organizando cada componente, temos:

0 = I O x ω x

8,4853 = I O y ω y

- 8,4853 = I O z ω z

Vamos imaginar um novo sistema de coordenadas que passa no centro da placa ( x ' , y ' , z ' ) .

Os momentos de inercia do disco com relação ao centroide são dados por:

I x ' = I z ' = I y ' = 1 12 m l 2

I x ' = 1 12 7,5 0,36 2

I x ' = 0,081

I y ' = 1 12 7,5 0,36 + 0,12 2

I y ' = 0,144   k g ⋅ m 2

I z ' = 1 12 7,5 0,12 2

I z ' = 9 10 - 3

Por simetria sabemos que I x ' y ' = I y ' z ' = I x ' z ' = 0 .

Temos:

u x ' = cos ⁡ 71,57 ° = 0 , 3162

u y ' = cos ⁡ 90 ° = 0

u z ' = cos ⁡ 18,43 ° = 0 , 9487

Temos que:

I z = I x ' u x ' 2 + I y ' u y ' 2 + I z ' u z ' 2 - 2 I x ' y ' u x ' u y ' - 2 I y ' z ' u y ' u z ' - 2 I x ' z ' u x ' u z '

I z = 0,081 0,3162 2 + 0,144 ( 0 ) + 9 10 - 3 0,9487 1 2 - 0 - 0 - 0

I z = 0,0162   k g ⋅ m 2

Aplicando conservação de trabalho e energia, temos:

T 1 = ∑ U 1 → 2 = T 2

0 + 40 0,36 sin ⁡ 18,43 ° 2 π = 1 2 0,0162   ω 3

ω = 59,4   r a d / s

Resposta

ω = 59,4   r a d / s

Ver Outros Exercícios desse livro