Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 1
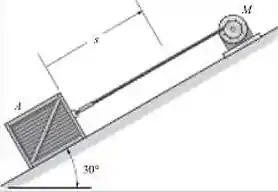
O motor enrola o cabo com uma acelareção constante de tal maneira que a caixa de kg se move em uma distância m em s, partindo do repouso. Determine a tração desenvolvida no cabo. O coeficiente de atrito cinético entre a caixa e o plano é .
Passo 1
Na primeira etapa de solução do problema, sabemos que o bloco de kg se move a uma aceleração constante partindo do repouso, sendo assim, podemos aplicar a equação do movimento para aceleração contante, neste caso:
Passo 2
O problema nos diz que o bloco parte do repouso logo: , e . Assim, equação pode ser simplificada e a aceleração calculada,
Isolando a aceleração:
Agora vamos substituir os valores fornecidos no problema e :
Passo 3
Na segunda etapa de solução do problema, devemos encontrar as forças atuantes no bloco através de um diagrama de corpo livre (DCL):
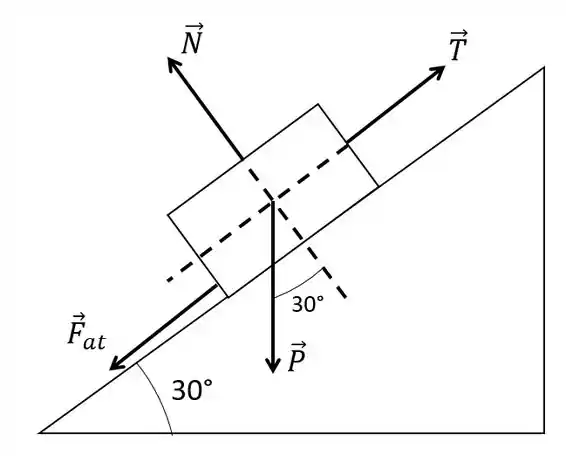
Além disso vamos decompor a força peso nas direções paralela ao plano e perpendicular a ele. Aqui é importante lembrar que e são componentes, paralela eperpendicular ao plano, respectivamente, da força peso.
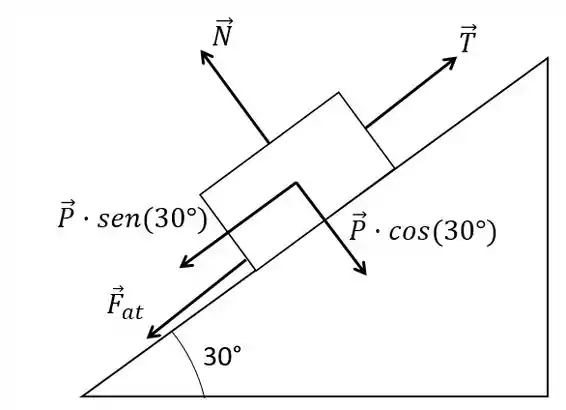
Para facilitar o desenvolvimento das equações do movimento, utilizaremos um sistema de coordenada onde as direções dos eixos e serão iguas as direções da tração, , e normal, , respectivamente.
Passo 4
Aplicando a segunda lei de Newton na direção ,
Passo 5
Aplicando a segunda lei de Newton na direção ,
Resposta
A tração desenvolvida no cabo é aproximadamente N.