Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 83

Uma placa de aço, com 160   m m de largura e 8   m m de espessura, é dobrada para formar a viga em forma de U mostrada na figura . Sabendo que a força vertical P atua em um ponto do plano médio da alma do U . determine (a) o torque T que faria o U torcer da mesma maneira como faz sob a carga P e b a tensão de cisalhamento máxima no U provocada pela força P .

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine o torque T que faria o U torcer da mesma maneira como faz sob a carga P e a tensão de cisalhamento máxima no U provocada pela força P . Os dados do enunciado são apresentados abaixo:

b = 30   m m                       h = 100   m m                           t = 8   m m .

e = b 2 + h 3 b = 30 2 + 100 3 30 = 9,6429   m m = 9,6429 × 10 - 3 m

Passo 2

Para determinarmos a inercia temos:

I = 1 12 t h 2 6 b + h = 1 12 8 100 2 16 30 + 100 = 1,86667 × 10 6   m m 4 = 1,86667 × 10 - 6   m 4

Considere:   V = 15 × 10 3 N

Então, para (a) teremos o seguinte, vamos começar calculando o torque:

T = V e = 15 × 10 3 9,6429 × 10 - 3 = 144,6   N / m

Agora calculamos a tensão na linha neutra devido a V, como o esboço abaixo:

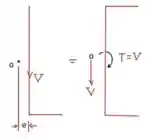
Q = b t h 2 + t h 2 h 4 = 1 8 t h h + 4 b = 1 8 8 100 100 + 4 30 = 22 × 10 3   m m 3 = 22 × 10 - 6   m 3

Considerando: t = 8 × 10 - 3 m podemos determinar a tensão de cisalhamento ;)

τ V = V Q I t = 15 × 10 3 22 × 10 - 6 1,86667 × 10 - 6 8 × 10 - 3 = 22,10 × 10 6   P a = 22,10   M P a

Muito bem… agora calculamos a tensão:

a = 2 b + h = 160   m m = 0,160   m

c 1 = 1 3 1 - 0,630 t a = 1 3 1 - 0,630 8 160 = 0,3228

τ V = T c 1 a t 2 = 144,64 0,3228 0,160 8 × 10 - 3 2 = 43,76 × 10 6   P a = 43,76   M P a

Passo 3

E finalizando, temos como resposta de (b) através de superposição, temos:

τ m a x = τ V + τ T

τ m a x = 22,10 + 43,76 =   65,9   M P a

Resposta

  1. T = 144,6   N / m
  2. τ m a x = 65,9   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de madeira de 152,4m mx304,8m m foi reforçada aparafusando-se nela o reforço de aço mostrado na figura. O modulo de elasticidade para a madeira é de 12,4G P a , e para o aço de 200G P a . Sab
Para a barra composta indicada, determine o raio de curvatura provocado pelo momento fletor de 50,8k N m
A viga de concreto reforçado mostrada na figura está submetida a um momento fletor positivo de 175 kNm. Sabendo que o módulo de elasticidade é de 25G P a para o concreto e de 200G P a para o aço, dete
Resolva o problema 4.49 considerando que a largura de 300 m m seja aumentado para 350m m .
Resolver o problema 4.47 assumindo que o espaçamento do diâmetro de 5 / 8( 15,88 m m ) da barra de aço é aumentada para 7,5i n( 190,5m m ) .