Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 118

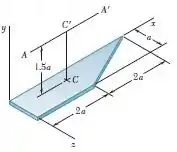
Uma placa delgada de massa m tem o formato trapezoidal mostrado na figura. Determine o momento de inércia de massa da placa em relação a ao eixo centroidal C C ' perpendicular à placa, b ao eixo A A ' paralelo ao eixo x e localizado a uma distância 1,5 a da placa.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiramente, observe a placa. Vamos dividi-la em duas partes para calcular a sua massa em dunção da densidade. Uma parte quadrada e outra triangular e calcular o momento de inércia em x :

I x = I x , 1 + I x , 2

I x = 1 3 2 a a 3 + 1 12 2 a a 3

I x = 5 6 a 4

Transformando o momento de inércia em função da geometria para momento de inércia em função da massa, temos:

I x ,   m a s s a = m A I x

I x ,   m a s s a = m 2 a a + 2 a a 2 5 6 a 4

I x ,   m a s s a = 5 18 m a 2

Passo 2

No item anterior, as duas partes que separamos da peça passam pelo eixo x . Agora, somente a parte quadrada passa pelo eixo z . Sendo assim, precisamos, além da soma das duas inércias, considerar eixos paralelos para a inércia da parcela que não passa pelo eixo.

I z = I z , 1 + I z , 2

I z = I z , 1 + I z ' , 2 + I z , 2

I z = 1 3 b h 3 + 1 36 v h 3 + 1 2 b h d 2

I z = 1 3 2 a a + 1 36 a 2 a + 1 2 2 a a 2 a + 1 3 2 a 2

I z = 10 a 4

Logo:

I z ,   m a s s a = m A I z

I z ,   m a s s a = m 2 a a + 2 a a 2 10 4

I z ,   m a s s a = 10 3 m a 2

Passo 3

Agora podemos calcular o momento de inércia em relação a y pela soma dos momentos de inércia dos eixos x e z :

I y ,   m a s s a = I x ,   m a s s a + I z ,   m a s s a

I y ,   m a s s a = 5 18 m a 2 + 10 3 m a 2

I y ,   m a s s a = 65 18 m a 2

Passo 4

Agora, vamos encontrar o centro da placa, para podermos definir o eixo centroidal paralelo que o exercício nos pede:

X = ∑ x A A

X = a 2 a 2 + 2 a 3 + 2 a 2 a 2 2 2 a 2 + 2 a 2 2

X = 14 9 a

E:

Z = a 2 2 a 2 + 1 3 a 2 a 2 2 2 a 2 + 2 a 2 2

Z = 4 9 a

Passo 5

Por fim, podemos encontrar o momento de inércia do componente em relação ao eixo central C C ' paralelo a y :

I y ' , m a s s a = I C C ' ,   m a s s a + m X 2 + Z 2

Logo:

I C C ' ,   m a s s a = I y ' , m a s s a - m X 2 + Z 2

I C C ' ,   m a s s a = 65 18 m a 2 - m 14 9 a 2 + 4 9 a 2

I C C ' ,   m a s s a = 0,994 m a 2

Passo 6

Agora, vamos considerar o eixo paralelo X , na distância que o problema nos propõe:

I A A ' , m a s s a = I x , m a s s a + m 1,5 a 2 + Z 2

I A A ' , m a s s a = 2,33 m a 2

Resposta

a ) I C C ' ,   m a s s a = 0,994 m a 2

b ) I A A ' , m a s s a = 2,33 m a 2

Ver Outros Exercícios desse livro