Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 33

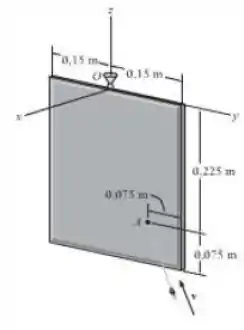
A placa fina de 12,5 kg está suspensa por uma junta esférica em O. Um projétil de 0,1 kg é disparado com uma velocidade v = - 90 i - 75 j + 90 k   m / s sobre a placa e fica embutido na placa no ponto A. Determine a velocidade angular da placa logo após o impacto e o eixo em torno do qual ela começa a girar. Despreze a massa do projétil após ele se embutir na placa.

Passo 1

Temos um problema de cinética de corpo rígido. Problemas deste tipo requerem muito cuidado para não errarmos uma pequena conta ou esquecermos algum parâmetro.

Começaremos determinando todos os parâmetros geométricos do nosso problema: produtos e momentos de inércia. Depois, precisaremos determinar a quantidade de movimento angular em relação ao ponto fixo O logo antes do impacto. Para isto, basta utilizarmos a seguinte relação:

H O i = r A / O × m p v p

Depois, para determinarmos a velocidade angular da placa, precisaremos calcular a quantidade de movimento angular após o impacto da bala. Mas sim, como que vamos calcular se nós não temos a velocidade angular??? É pegadinha?? Claro que não! Basta lembrarmos que o momento angular é conservador após o impacto! Isto é:

H O i = H O f

Agora sim!! E após calcularmos a velocidade angular, o eixo por onde passa é dado exatamente pelo vetor velocidade angular! O que iremos fazer é apenas normalizar este vetor.

Passo 2

Vamos começar determinando os momentos de inércia e produtos de inércia do nosso satélite. Como é uma placa fina, vamos utilizar as relações geométricas já calculadas no final do livro. Portanto, temos os seguintes momentos de inércia:

I x ' = 1 12 m a 2 + b 2 + m l 2 = 1 12 ⋅ 12,5 ⋅ 0,3 2 + 0,3 2 + 12,5 ⋅ 0,15 2 = 0,46875   k g ⋅ m 2

I y ' = 1 12 m a 2 + m l 2 = 1 12 ⋅ 12,5 ⋅ 0,3 2 + 12,5 ⋅ 0,15 2 = 0,375   k g ⋅ m 2

I z ' = 1 12 m b 2 = 1 12 ⋅ 12,5 ⋅ 0,3 2 = 0,09375   k g ⋅ m 2

Agora, precisamos determinar os produtos de inércia. Só que, neste caso, temos uma característica especial no nosso satélite: ele é simétrico. Portanto, os produtos de inércia são nulos! Isto é:

I x ' y ' = I x ' z ' = I y ' z ' = 0

Mais fácil não é!

Passo 3

Vamos calcular agora a quantidade de movimento angular antes do impacto da bala. Para isto, precisamos escrever antes quem é o vetor r A / O , que tem início em O e extremidade em A. Logo,

r A / O = 0,15 - 0,075 j - 0,225 k   m

r A / O = 0,075 j - 0,225 k   m

Agora, basta aplicarmos na equação definida no passo 1. Portanto,

H O i = r A / O × m p v p = i j k 0 0,075 - 0,225 0,1 ⋅ - 90 0,1 ⋅ - 75 0,1 ⋅ 90

Calculando o determinante da matriz acima, obtemos:

H O i = - 1,0125 i + 2,025 j + 0,675 k   k g ⋅ m 2 / s

Passo 4

Agora precisamos determinar a quantidade de movimento angular após o impacto da bala. Sabendo que a velocidade angular é dada por:

ω = ω x i + ω y j + ω z k

A quantidade de movimento angular será dada por:

H O f = I x ' ⋅ ω x + I y ' ⋅ ω y + I z ' ⋅ ω z

H O f = 0,46875   ⋅ ω x i + 0,375 ⋅ ω y j + 0,09375 ⋅ ω z k

Por causa da conservação do momento, temos:

H O i = H O f

- 1,0125 i + 2,025 j + 0,675 k = 0,46875   ⋅ ω x i + 0,375 ⋅ ω y j + 0,09375 ⋅ ω z k

Logo, obtemos:

ω x = - 2,16   r a d / s

ω y = 5,4   r a d / s

ω z = 7,2   r a d / s

Passo 5

O eixo no qual a placa irá girar é dado exatamente pelo vetor velocidade angular, isto é:

v = ω = ( - 2,16 i + 5,4 j + 7,2 k )

Vamos apenas normalizar este vetor, isto é, escrever o seu versor. Obtemos então:

u = - 2,16 i + 5,4 j + 7,2 k 2,16 2 + 5,4 2 + 7,2 2

u = - 0,233 i + 0,583 j + 0,778 k

Resposta

ω = - 2,16 i + 5,4 j + 7,2 k   r a d / s

Eixo pelo qual a placa gira:

u = - 0,233 i + 0,583 j + 0,778 k

Ver Outros Exercícios desse livro