Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 31
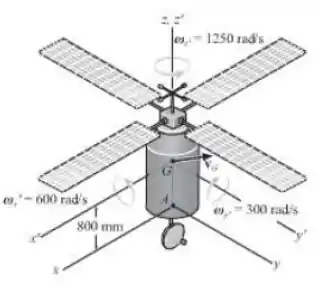
O satélite de 200 kg tem seu centro de massa no ponto G. Seus raios de giração em relação aos eixos , , são , , respectivamente. No instante mostrado, o satélite gira em torno dos eixos , e com a velocidade angular mostrada e seu centro de massa G tem uma velocidade . Determine a quantidade de movimento angular do satélite em relação ao ponto A nesse instante.
Passo 1
Temos um problema de cinética de corpo rígido. Problemas deste tipo requerem muito cuidado para não errarmos uma pequena conta ou esquecermos algum parâmetro.
Começaremos determinando todos os parâmetros geométricos do nosso problema: produtos e momentos de inércia. Depois, determinaremos a quantidade de movimento angular em torno do centro de massa, isto é, .
Com este valor, podemos calcular facilmente a quantidade de movimento em torno do ponto A, basta lembrarmos da seguinte equação vetorial:
Em que é um vetor que tem início em A e extremidade em G!
Passo 2
Vamos começar determinando os momentos de inércia e produtos de inércia do nosso satélite. Como já nos foi dado o raio de giração em relação aos eixos que passam pelo centro de massa, temos os seguintes momentos de inércia:
Agora, precisamos determinar os produtos de inércia. Só que, neste caso, temos uma característica especial no nosso satélite: ele é simétrico. Portanto, os produtos de inércia são nulos! Isto é:
Mais fácil não é!
Passo 3
Agora que determinamos os paramétricos geométricos do nosso problema, podemos calcular a quantidade de movimento do seu centro de massa. Para isto, vamos ter de utilizar a velocidade angular do satélite. Diretamente do gráfico, temos a seguinte velocidade:
Muito cuidado na hora de extraírem os valores do gráfico! O sinal é de extrema importância!!! Chequem sempre a regra da mão direita!
Agora, podemos calcular facilmente a quantidade de movimento angular. Basta multiplicarmos o produto de inércia de cada um dos eixos pela componente da velocidade angular relacionada ao eixo, isto é:
Como o momento angular é uma grandeza vetorial, podemos escrevê-lo da seguinte forma:
Passo 4
Estamos quase acabando! Precisamos aplicar a equação descrita no Passo 1 para obtermos a quantidade de momento angular em relação ao ponto A, só precisamos calcular alguns parâmetros antes! Começaremos pelo vetor , que tem extremidade em G e início em A. Ele é dado por:
Agora, vamos fazer o produto vetorial entre este vetor e . Temos então:
Basta calcularmos o determinante desta matriz 3x3. Logo, obtemos:
Portanto, o nosso resultado final é: